
题目列表(包括答案和解析)
(本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,
![]() ;(1)求数列
;(1)求数列![]() 的通项公式
的通项公式
(2)设数列![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() (3)若(2)问中数列
(3)若(2)问中数列![]() 满足
满足 ![]() ,
,
求证: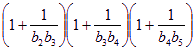
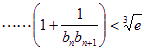 (其中
(其中![]() 为自然对数的底数)。
为自然对数的底数)。
(本小题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
[来源:学|科|网] |
|
合计 |
|
|
50[] |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为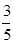
(1)请将上面的列联表补充完整
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球,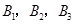
还喜欢打乒乓球,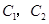 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、
喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求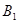 和
和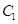 不全被选
不全被选
中的概率.
下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段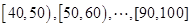 ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.[来源:学#科#网]
(本小题满分12分)
道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车. 某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:
(1)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(2)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;
(3)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的。依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率。(精确到0.01)并针对你的计算结果对驾驶员发出一句话的倡议.
(本小题满分12分)
2011年4月28日,世界园艺博览会已在西安正式开园,正式开园前,主办方安排了4次试运行,为了解前期准备情况和试运行中出现的问题,以做改进,组委会组织了一次座谈会,共邀请20名代表参加,他们分别是游客15人,志愿者5人。
(I)从这20名代表中随机选出3名谈建议,求至少有1人是志愿者的概率;
(II)若随机选出2名代表发言,![]() 表示其游客人数,求
表示其游客人数,求![]() 的分布列和数学期望。
的分布列和数学期望。
一、DDBCD CABCA
二、11.1;
12. ; 13.
; 13. 14.
14. ; 15.
; 15. ;
;
16.
三.解答题(本大题共6小题,共76分)
17.解:(1)法一:由题可得 ;
;
法二:由题 ,
,
故 ,从而
,从而 ;
;
法三:由题 ,解得
,解得 ,
,
故 ,从而
,从而 。
。
(2) ,令
,令 ,
,
则 ,
,
 在
在 单调递减,
单调递减,
故
 ,
,
从而 的值域为
的值域为 。
。
18.解:(1) 的可能取值为0,1,2,3,4,
的可能取值为0,1,2,3,4, ,
,

 ,
,
 ,
, ,
,
 。
。
因此随机变量 的分布列为下表所示;
的分布列为下表所示;

0
1
2
3
4






(2)由⑴得: ,
,

19.法一:(1)连接 ,设
,设 ,则
,则 。
。
因为 ,所以
,所以 ,故
,故 ,从而
,从而 ,
,
故 。
。
又因为 ,
,
所以 ,当且仅当
,当且仅当 取等号。
取等号。
此时 为
为 边的中点,
边的中点, 为
为 边的中点。
边的中点。
故当 为
为 边的中点时,
边的中点时, 的长度最小,其值为
的长度最小,其值为
(2)连接 ,因为此时
,因为此时 分别为
分别为 的中点,
的中点,
故 ,所以
,所以 均为直角三角形,
均为直角三角形,
从而 ,所以
,所以 即为直线
即为直线 与平面
与平面 所成的角。
所成的角。
因为 ,所以
,所以 即为所求;
即为所求;
(3)因 ,又
,又 ,所以
,所以 。
。
又 ,故三棱锥
,故三棱锥 的表面积为
的表面积为
 。
。
因为三棱锥 的体积
的体积 ,
,
所以 。
。
法二:(1)因 ,故
,故 。
。
设 ,则
,则 。
。
所以 ,
,
当且仅当 取等号。此时
取等号。此时 为
为 边的中点。
边的中点。
故当 为
为 的中点时,
的中点时, 的长度最小,其值为
的长度最小,其值为 ;
;
(2)因 ,又
,又 ,所以
,所以 。
。
记 点到平面
点到平面 的距离为
的距离为 ,
,
因 ,故
,故 ,解得
,解得 。
。
 因
因 ,故
,故 ;
;
(3)同“法一”。
法三:(1)如图,以 为原点建立空间直角坐标系,设
为原点建立空间直角坐标系,设 ,则
,则 ,
,
所以 ,当且仅当
,当且仅当 取等号。
取等号。
此时 为
为 边的中点,
边的中点, 为
为 边的中点。
边的中点。
故当 为
为 边的中点时,
边的中点时, 的长度最小,其值为
的长度最小,其值为 ;
;
(2)设 为面
为面 的法向量,因
的法向量,因 ,
,
故 。取
。取 ,得
,得 。
。
又因 ,故
,故 。
。
因此 ,从而
,从而 ,
,
所以 ;
;
(3)由题意可设 为三棱锥
为三棱锥 的内切球球心,
的内切球球心,
则 ,可得
,可得 。
。
与(2)同法可得平面 的一个法向量
的一个法向量 ,
,
又 ,故
,故 ,
,
解得 。显然
。显然 ,故
,故 。
。
20.解:(1)当 时,
时, 。令
。令 得
得 ,
,
故当 时
时 ,
, 单调递增;
单调递增;
当 时
时 ,
, 单调递减。
单调递减。
所以函数 的单调递增区间为
的单调递增区间为 ,
,
单调递减区间为 ;
;
(2)法一:因 ,故
,故 。
。
令 ,
,
要使 对满足
对满足 的一切
的一切 成立,则
成立,则 ,
,
解得 ;
;
法二: ,故
,故 。
。
由 可解得
可解得 。
。
因为 在
在 单调递减,因此
单调递减,因此 在
在 单调递增,故
单调递增,故 。设
。设 ,
,
则 ,因为
,因为 ,
,
所以 ,从而
,从而 在
在 单调递减,
单调递减,
故 。因此
。因此 ,即
,即 。
。
(3)因为 ,所以
,所以
即 对一切
对一切 恒成立。
恒成立。
 ,令
,令 ,
,
则 。因为
。因为 ,所以
,所以 ,
,
故 在
在 单调递增,有
单调递增,有 。
。
因此 ,从而
,从而 。
。
所以 。
。
21.解:(1)设 ,则由题
,则由题 ,
,
由 得
得 ,故
,故 。
。
又根据 可得
可得 ,
,
即 ,代入可得
,代入可得 ,
,
解得 (舍负)。故
(舍负)。故 的方程为
的方程为 ;
;
(2)法一:设 ,代入
,代入 得
得 ,
,
故 ,
,
从而


因此 。
。
法二:显然点 是抛物线
是抛物线 的焦点,点
的焦点,点 是其准线
是其准线 上一点。
上一点。
设 为
为 的中点,过
的中点,过 分别作
分别作 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
则 。
。
因此以 为直径的圆与准线
为直径的圆与准线 相切(于点
相切(于点 )。
)。
若 与
与 重合,则
重合,则 。否则点
。否则点 在
在 外,因此
外,因此 。
。
综上知 。
。
22.证明:(1)因 ,故
,故 。
。
显然 ,因此数列
,因此数列 是以
是以 为首项,以2为公比的等比数列;
为首项,以2为公比的等比数列;
(2)由⑴知 ,解得
,解得 ;
;
(3)因为

所以 。
。
又
 (当且仅当
(当且仅当 时取等号),
时取等号),
故 。
。
综上可得 。(亦可用数学归纳法)
。(亦可用数学归纳法)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com