
题目列表(包括答案和解析)
如图,在四棱锥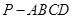 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,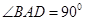 ,
, ,
,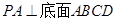 ,且PA=AD=DC=
,且PA=AD=DC= AB=1.
AB=1.
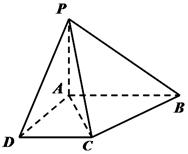
(1)证明:平面 平面
平面
(2)设AB,PA,BC的中点依次为M、N、T,求证:PB∥平面MNT
(3)求异面直线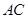 与
与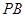 所成角的余弦值
所成角的余弦值
如图,正四棱柱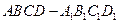 中,
中,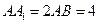 ,点
,点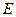 在
在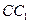
 上且
上且
(1)证明: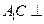 平面
平面 ;
;
(2)求二面角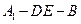 的余弦值.
的余弦值.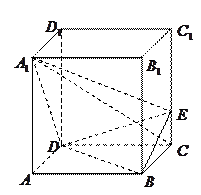
(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足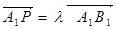
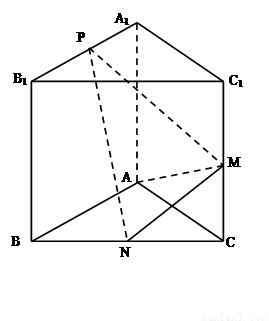
(1)证明:PN⊥AM
(2)若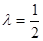 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.
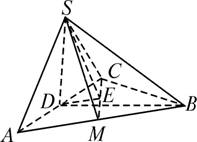
(1)证明AC⊥SB;
(2)求二面角S-CM-A的大小;
(3)求点B到平面SCM的距离.
已知坐标平面内两点A=(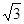 ,-1), B=(
,-1), B=(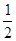 ,
,
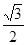 ),O为原点。
),O为原点。
(1)证明OA⊥OB;
(2)设a =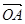 ,b=
,b=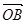 ,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com