练习册

  • 练习册
  • 试题
    (1)证明:设=a.=b.=c.则|a|=|b|.∵=b-a. ∴·=(b-a)·c=b·c-a·c=|b|·|c|cos60°-|a|·|c|cos60°=0. ∴C1C⊥BD. (2)解:连AC.BD.设AC∩BD=O.连OC1.则∠C1OC为二面角α-BD-β的平面角. ∵(a+b).(a+b)-c ∴·(a+b)·［(a+b)-c］ =(a2+2a·b+b2)-a·c-b·c =-·2·cos60°-·2·cos60°=. 则||=.||=.∴cosC1OC= (3)解:设=x.CD=2. 则CC1=. ∵BD⊥平面AA1C1C.∴BD⊥A1C ∴只须求满足:=0即可. 设=a.=b.=c. ∵=a+b+c.=a-c. ∴=(a+b+c)(a-c)=a2+a·b-b·c-c2=-6.令6-=0.得x=1或x=-. 评述:本题蕴涵着转化思想.即用向量这个工具来研究空间垂直关系的判定.二面角的求解以及待定值的探求等问题. 【查看更多】

     

    题目列表(包括答案和解析)

    用反证法证明：“若m∈Z且m为奇数，则2m±均为奇数”，其假设正确的是

    A.都是偶数         B.不都是奇数        C.都不是奇数        D.都不是偶数

    查看答案和解析>>

    用反证法证明：“若m∈Z且m为奇数，则2m±均为奇数”，其假设正确的是

    A.都是偶数                                 B.不都是奇数

    C.都不是奇数                               D.都不是偶数

    查看答案和解析>>

    用反证法证明：“方程ax2＋bx＋c＝0，且a，b，c都是奇数，则方程没有整数根”正确的假设是方程存在实数根x0为

    [　　]
    A．

    整数

    B．

    奇数或偶数

    C．

    正整数或负整数

    D．

    自然数或负整数

    查看答案和解析>>

    完成下列证明，已知直线a、b、c不共面，它们相交于点P，AÎa，DÎa，BÎb，EÎc

    求证：BD和AE是异面直线

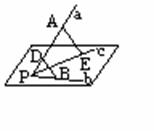
    证明：假设__   共面于g，则点A、E、B、D都在平面_     _内

      QAÎa，DÎa，∴__Ìγ.   QPÎa，∴PÎ__.

    QPÎb，BÎb，PÎc，EÎc  ∴_   _Ìg，   __Ìg，这与____矛盾 

    ∴BD、AE__________

    查看答案和解析>>

    完成下列证明，已知直线a、b、c不共面，它们相交于点P，A∈a，D∈a，B∈b，E∈c，求证：BD和AE是异面直线．

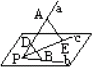
    证明：假设________共面于γ，则点A、E、B、D都在平面________内．

    Q A∈a，D∈a，∴________γ．

    Q P∈a，∴P∈________．

    Q P∈b，B∈b，P∈c，E∈c

    ∴________γ，________γ，这与________矛盾．

    ∴BD、AE________．

    查看答案和解析>>


    同步练习册答案