
题目列表(包括答案和解析)
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求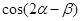 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴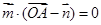 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,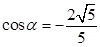 ,
,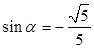 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即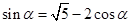 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
|
零件的个数 |
2 |
3 |
4 |
5 |
|
加工的时间 |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散点图;
(2)求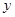 关于
关于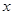 的线性回归方程
的线性回归方程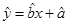 ;
;
(3)试预测加工10个零件需要多少时间?
(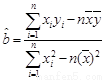 ,
,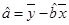 )
)
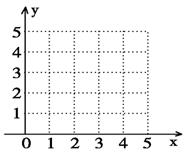
【解析】第一问中,利用表格中的数据先作出散点图
第二问中,求解均值a,b的值,从而得到线性回归方程。
第三问,利用回归方程将x=10代入方程中,得到y的预测值。
解:(1)散点图(略) (2分)
(2)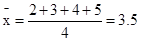
 (4分)
(4分)

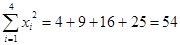 ∴
∴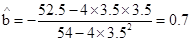 (7分)
(7分)
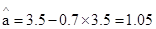 (8分)∴回归直线方程:
(8分)∴回归直线方程: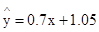 (9分)
(9分)
(3)当 ∴预测加工10个零件需要8.05小时。
∴预测加工10个零件需要8.05小时。
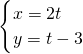 中消去t,此过程如下:
中消去t,此过程如下: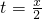 ,将
,将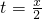 代入y=t-3中,得到
代入y=t-3中,得到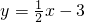 .
.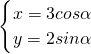 中的α消去,并说明它表示什么图形,求出其焦点.
中的α消去,并说明它表示什么图形,求出其焦点. 中消去t,此过程如下:
中消去t,此过程如下: ,将
,将 代入y=t-3中,得到
代入y=t-3中,得到 .
. 中的α消去,并说明它表示什么图形,求出其焦点.
中的α消去,并说明它表示什么图形,求出其焦点.在△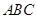 中,∠
中,∠ ,∠
,∠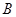 ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且
 .
.
(1)求∠ 的大小;(2)若
的大小;(2)若 ,
, ,求
,求 和
和 的值.
的值.
【解析】第一问利用余弦定理得到
 第二问
第二问
(2) 由条件可得 
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com