
题目列表(包括答案和解析)
设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在椭圆上且异于
在椭圆上且异于 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)若直线 与
与 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若 ,证明直线
,证明直线 的斜率
的斜率
 满足
满足
【解析】(1)解:设点P的坐标为 .由题意,有
.由题意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以椭圆的离心率
,所以椭圆的离心率
(2)证明:(方法一)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由条件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由P在椭圆上,有
因为 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
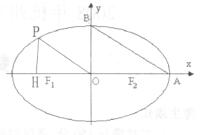
(08年杭州市质检二)(14分)如图,在椭圆![]() 中,点
中,点![]() 是左焦点,
是左焦点, ![]() ,
,![]() 分别为右顶点和上顶点,点
分别为右顶点和上顶点,点![]() 为椭圆的中心。又点
为椭圆的中心。又点![]() 在椭圆上,且满足条件:
在椭圆上,且满足条件:![]() ,点
,点![]() 是点
是点![]() 在x轴上的射影。
在x轴上的射影。
(1)求证:当![]() 取定值时,点
取定值时,点![]() 必为定点;
必为定点;
(2)如果点![]() 落在左顶点与左焦点之间,试求椭圆离心率的取值范围;
落在左顶点与左焦点之间,试求椭圆离心率的取值范围;
(3)如果以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,且凸四边形
相切,且凸四边形![]() 的面积等于
的面积等于![]() ,求椭圆的方程。
,求椭圆的方程。
已知椭圆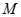 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0, ),(0,
),(0,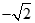 ),又点
),又点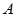
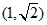 在椭圆
在椭圆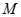 上.
上.
(1)求椭圆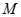 的方程;
的方程;
(2)已知直线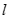 的斜率为
的斜率为 ,若直线
,若直线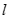 与椭圆
与椭圆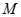 交于
交于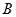 、
、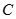 两点,求
两点,求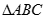 面积的最大值.
面积的最大值.
2.A解析:由![]() 知函数在
知函数在![]() 上有零点,又因为函数在(0,+
上有零点,又因为函数在(0,+![]() )上是减函数,所以函数y=f(x) 在(0,+
)上是减函数,所以函数y=f(x) 在(0,+![]() )上有且只有一个零点不妨设为
)上有且只有一个零点不妨设为![]() ,则
,则![]() ,又因为函数是偶函数,所以
,又因为函数是偶函数,所以![]() =0并且函数在(0,+
=0并且函数在(0,+![]() )上是减函数,因此-
)上是减函数,因此-![]() 是(-
是(-![]() ,0)上的唯一零点,所以函数共有两个零点
,0)上的唯一零点,所以函数共有两个零点
下列叙述中,是随机变量的有( )
①某工厂加工的零件,实际尺寸与规定尺寸之差;②标准状态下,水沸腾的温度;③某大桥一天经过的车辆数;④向平面上投掷一点,此点坐标.
A.②③ B.①② C.①③④ D.①③
(09年东城区期末理)(13分)
已知椭圆![]() 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线![]() 的焦点是椭圆
的焦点是椭圆![]() 的一个焦点,又点
的一个焦点,又点![]()
![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 的方向向量为
的方向向量为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com