
题目列表(包括答案和解析)
(08年浙江卷文)(本题14分)一个袋中装有大小相同的黑球、白球和红球。已知袋中共有10个球.从袋中任意摸出1个球,得到黑球的概率是![]() ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是![]() .求:
.求:
(Ⅰ)从中任意摸出2个球,得到的都是黑球的概率;
(Ⅱ)袋中白球的个数.
(本题14分)如图,直线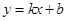 与椭圆
与椭圆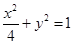 交于
交于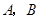 两点,记
两点,记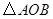 的面积为
的面积为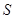 .
.
(I)求在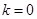 ,
,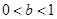 的条件下,
的条件下,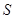 的最大值;
的最大值;
(II)当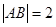 ,
,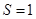 时,求直线
时,求直线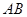 的方程.
的方程.

..(本题14分)已知 为常数,且
为常数,且 ,函数
,函数 ,
, (
( ,为自然对数的底数)
,为自然对数的底数)
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)当 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( <
< ),使得对每一个
),使得对每一个 ,直线
,直线 与曲线
与曲线 (
( )都有公共点?若存在,求出最小的实数
)都有公共点?若存在,求出最小的实数 和最大的实数
和最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(08年浙江卷文)(本题14分)已知数列![]() 的首项
的首项![]() ,通项
,通项![]() ,且
,且![]() 成等差数列.求:
成等差数列.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ) 数列![]() 前n项和
前n项和![]() 的公式.
的公式.
(本题14分) 如图,
如图,![]() 分别是正方体
分别是正方体![]() 的
的
棱![]() 的中点.
的中点.
(1)求证:![]() //平面
//平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com