
题目列表(包括答案和解析)
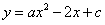 的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。
的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。 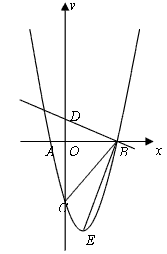
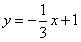 交y轴于D点,E为抛物线顶点。若
交y轴于D点,E为抛物线顶点。若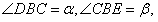 求
求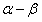 的值;
的值;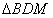 的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。
的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。 已知:二次函数![]() 的图象与X轴交于A(1,0)、B(5,0),抛物线的顶点为P,且PB=
的图象与X轴交于A(1,0)、B(5,0),抛物线的顶点为P,且PB=![]() ,
,
求:(1)二次函数的解析式。
(2)求出这个二次函数的图象;
(3)根据图象回答:当x取什么值时,y的值不小于0。
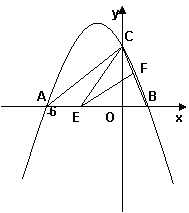
已知:二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
 |
1.
已知二次函数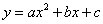 的图象与
的图象与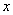 轴交于点(-2,0)、(
轴交于点(-2,0)、( ,0),且
,0),且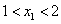 ,与y轴的正半轴的交点在(0,2)的下方.下列结论:①
,与y轴的正半轴的交点在(0,2)的下方.下列结论:①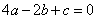 ;②
;②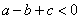 ;③
;③ ;④
;④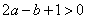 .其中正确结论的个数是( )个
.其中正确结论的个数是( )个
A.4个 B.3个 C.2个 D.1个
1. 已知二次函数![]() 的图象与
的图象与![]() 轴交于点(-2,0)、(
轴交于点(-2,0)、(![]() ,0),且
,0),且![]() ,与y轴的正半轴的交点在(0,2)的下方.下列结论:①
,与y轴的正半轴的交点在(0,2)的下方.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数是( )个
.其中正确结论的个数是( )个
A.4个 B.3个 C.2个 D.1个
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
D
C
A
D
B
D
B
C
A
B
二、填空题
13、 14、
14、 15、
15、
16、3cm 17、 18、x=5 19、4:5
18、x=5 19、4:5
20、解原式=
= -
- +1+1=2
+1+1=2
21、证略
22、解(1)由题意,设二次函数的解析式为y=a(x-1)(x-5),即y=ax2-6ax+5a
对称轴为x=3,设对称轴与x轴的交点为C(3,0)
∴OC=3 ∵OB=5 ∴BC=2
∵P是顶点,BP= ∴PC=4 P(3,-4)
∴PC=4 P(3,-4)
∴ ∴
∴
∴二次函数的解析式为
(2)略 (3)当1<x<5时,y<0
23、(1)240-x,x-40,300-x
(2)w=9200+2x(40≤x≤2100)
W最小=9200+80=9280元
24、解:过E作EF⊥AB于F ∵AB⊥BC,DC⊥BC ∴四边形BCEF是矩形,
EF=BC=24,∠AEF=32°∵tan∠AEF= ∴AF=EF tan∠AEF=24×
∴AF=EF tan∠AEF=24× =15
=15
∴EC=BF=40-15=25,25÷25=10,故刘卉家住的楼层至少是10层。
25、(1)证明:连接CO并延长交⊙O于M,连接AM
∵PC2=PA.PB ∴
∵∠P=∠P ∴△PAC∽△PCB ∠PCA=∠B
∵∠B=∠M ∴∠M=∠PCA
∵CM是直径 ∴∠MAC=90° ∴∠ACM+∠M=90° ∴∠ACM+∠PCA=90°
即∠PCM=90° ∴CM⊥PC ∴PC是⊙O的切线。
(2)连接AO,并延长AO交⊙O于N,连接BN
∵AN是直径 ∴∠ABN=90° ∠N=∠ACB,AN=12
在Rt△ABN中,AB=ANsin∠ACB=12sin∠ACB=12× =
=
(3)连接OD交AB于F,∴OD⊥AB ∵D是劣弧AB的中点 ∴∠ACD=∠BCD
∵∠PCA=∠B ∴∠PCE=∠PEC ∴PC=PE 由△PCA∽△PBC 得 PC=3PA
∵PC2=PA.PB ∴9PA2=PA.PB ∴9PA=PB=PA+AB ∴8PA=AB=
∴PA= ∴PC=PE=
∴PC=PE=
AE= ,AB=
,AB= ,AF=
,AF= ,EF=
,EF=
在Rt△OAF中,可求得OF=4 ∴DF=2 DE=3
∵AE?EB=DE?CE ∴CE=5
26、解:(1)A(2,0)、B(10,0)、C(10,8)、D(2,8)
(2)过P作PE⊥X轴于E
∴PE=AE= BC=4 OE=6 ∴P(6,4)
BC=4 OE=6 ∴P(6,4)
设抛物线 ,即
,即
 ∴
∴
故二次函数的解析式为: ,顶点(5,
,顶点(5, )
)
(3)存在点Q使△QAB的面积为16,
Q1(4,4)、Q2(6,4)Q3(-2,-4)Q4(-4,12)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com