练习册

  • 练习册
  • 试题
    如图.在平面直角坐标系中.四边形ABCD是边长为8的正方形.OA=2.求:(1)写出A.B.C.D各点的坐标,(2)若正方形ABCD的两条对角线相交于点P.请求出经过O.P.B三点的抛物线垢解析式,中的抛物线上.是否存在一点Q.使△QAB的面积为16.如果存在.请求出Q点的坐标,如果不存在.请说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

    （本题12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．

    1.（1）当∠AOB=30°时，求弧AB的长度；

    2.（2）当DE=8时，求线段EF的长；

    3.（3）在点B运动过程中，当交点E在O，C之间时，是否存在以点E、C、F为顶点的三角形与△AOB相

    似，若存在，请求出此时点E的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    （本题12分）如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙G交x轴于D点，过点D作DF⊥AE于点F．

    （1）求OA、OC的长；

    （2）求证：DF为⊙G的切线；

    （3）小明在解答本题时，发现△AOE是等腰三角形．那么，直线BC上是否存在除点E以外的点P，使△AOP也是等腰三角形，如果存在，请直接写出所有符合题意的点P坐标．

     

    查看答案和解析>>

    （本题12分）如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙G交x轴于D点，过点D作DF⊥AE于点F．
    （1）求OA、OC的长；
    （2）求证：DF为⊙G的切线；
    （3）小明在解答本题时，发现△AOE是等腰三角形．那么，直线BC上是否存在除点E以外的点P，使△AOP也是等腰三角形，如果存在，请直接写出所有符合题意的点P坐标．

    查看答案和解析>>

    （本题12分）如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙G交x轴于D点，过点D作DF⊥AE于点F．
    （1）求OA、OC的长；
    （2）求证：DF为⊙G的切线；
    （3）小明在解答本题时，发现△AOE是等腰三角形．那么，直线BC上是否存在除点E以外的点P，使△AOP也是等腰三角形，如果存在，请直接写出所有符合题意的点P坐标．

    查看答案和解析>>

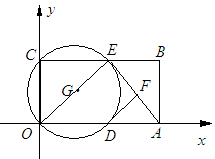
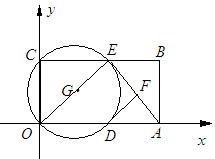
    （本题12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．

    1.（1）当∠AOB=30°时，求弧AB的长度；

    2.（2）当DE=8时，求线段EF的长；

    3.（3）在点B运动过程中，当交点E在O，C之间时，是否存在以点E、C、F为顶点的三角形与△AOB相

    似，若存在，请求出此时点E的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    一、选择题

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    C

    B

    D

    C

    A

    D

    B

    D

    B

    C

    A

    B

    二、填空题

    13、     14、     15、

    16、3cm    17、       18、x=5    19、4：5

     20、解原式=

              =-+1+1=2

    21、证略

    22、解（1）由题意，设二次函数的解析式为y=a(x-1)(x-5),即y=ax2-6ax+5a

          对称轴为x=3，设对称轴与x轴的交点为C(3,0)

         ∴OC=3      ∵OB=5     ∴BC=2

         ∵P是顶点，BP=   ∴PC=4    P（3，-4）

        ∴    ∴

        ∴二次函数的解析式为

       （2）略    （3）当1<x<5时，y<0

    23、(1)240-x,x-40,300-x

        (2)w=9200+2x(40≤x≤2100)

        W最小=9200+80=9280元

    24、解：过E作EF⊥AB于F     ∵AB⊥BC，DC⊥BC      ∴四边形BCEF是矩形，

         EF=BC=24，∠AEF=32°∵tan∠AEF=  ∴AF=EF tan∠AEF=24×=15

    ∴EC=BF=40-15=25，25÷25=10，故刘卉家住的楼层至少是10层。

    25、（1）证明：连接CO并延长交⊙O于M，连接AM

          ∵PC2=PA.PB     ∴    

     ∵∠P=∠P    ∴△PAC∽△PCB     ∠PCA=∠B

    ∵∠B=∠M  ∴∠M=∠PCA    

    ∵CM是直径 ∴∠MAC=90°  ∴∠ACM+∠M=90°  ∴∠ACM+∠PCA=90°

    即∠PCM=90°  ∴CM⊥PC  ∴PC是⊙O的切线。

      （2）连接AO，并延长AO交⊙O于N，连接BN

    ∵AN是直径   ∴∠ABN=90° ∠N=∠ACB，AN=12

    在Rt△ABN中，AB=ANsin∠ACB=12sin∠ACB=12×=

     （3）连接OD交AB于F，∴OD⊥AB   ∵D是劣弧AB的中点  ∴∠ACD=∠BCD

    ∵∠PCA=∠B  ∴∠PCE=∠PEC   ∴PC=PE   由△PCA∽△PBC 得 PC=3PA

    ∵PC2=PA.PB  ∴9PA2=PA.PB   ∴9PA=PB=PA+AB   ∴8PA=AB=

    ∴PA=    ∴PC=PE=

    AE=，AB=，AF=，EF=

    在Rt△OAF中，可求得OF=4    ∴DF=2   DE=3

    ∵AE?EB=DE?CE   ∴CE=5

    26、解：（1）A（2，0）、B（10，0）、C（10，8）、D（2，8）

      （2）过P作PE⊥X轴于E

          ∴PE=AE=BC=4      OE=6     ∴P（6，4）

         设抛物线，即

        ∴

    故二次函数的解析式为：，顶点（5，）

      （3）存在点Q使△QAB的面积为16，

    Q1（4，4）、Q2（6，4）Q3（-2，-4）Q4（-4，12） 

     

     

     


    同步练习册答案