练习册

  • 练习册
  • 试题
    解析:对于A为关于的不等式的解集.若.则有.因此有.则实数的取值范围为. 【查看更多】

     

    题目列表(包括答案和解析)

    解关于的不等式

    【解析】本试题主要考查了含有参数的二次不等式的求解，

    首先对于二次项系数a的情况分为三种情况来讨论，

    A=0,a>0,a<0,然后结合二次函数的根的情况和图像与x轴的位置关系，得到不等式的解集。

    解：①若a=0，则原不等式变为-2x+2<0即x>1

    此时原不等式解集为；   

    ②若a>0，则ⅰ）时，原不等式的解集为；

    ⅱ）时，原不等式的解集为；

      ⅲ）时，原不等式的解集为。 

    ③若a<0，则原不等式变为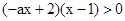

        原不等式的解集为。

     

    查看答案和解析>>

    三位同学合作学习，对问题“已知不等式xy≤ax2+2y2对于x∈[1，2]，y∈[2，3]恒成立，求a的取值范围”提出了各自的解题思路．
    甲说：“可视x为变量，y为常量来分析”．
    乙说：“寻找x与y的关系，再作分析”．
    丙说：“把字母a单独放在一边，再作分析”．
    参考上述思路，或自已的其它解法，可求出实数a的取值范围是（　　）
    A、[-1，6]B、[-1，4）C、[-1，+∞）D、[1，+∞）

    查看答案和解析>>

    三位同学合作学习，对问题“已知不等式xy≤ax2+2y2对于x∈[1，2]，y∈[2，3]恒成立，求a的取值范围”提出了各自的解题思路．
    甲说：“可视x为变量，y为常量来分析”．
    乙说：“寻找x与y的关系，再作分析”．
    丙说：“把字母a单独放在一边，再作分析”．
    参考上述思路，或自已的其它解法，可求出实数a的取值范围是
    [-1，+∞）
    [-1，+∞）
    ．

    查看答案和解析>>

    三位同学合作学习，对问题“已知不等式对于恒成立，求a的取值范围”提出了各自的解题思路.

    甲说：“可视为变量，为常量来分析”.

    乙说：“寻找与的关系，再作分析”.

    丙说：“把字母单独放在一边，再作分析”.

    参考上述思路，或自已的其它解法，可求出实数的取值范围是

    A．           B．        C．       D．

     

    查看答案和解析>>

    三位同学合作学习，对问题“已知不等式xy≤ax2+2y2对于x∈[1，2]，y∈[2，3]恒成立，求a的取值范围”提出了各自的解题思路．
    甲说：“可视x为变量，y为常量来分析”．
    乙说：“寻找x与y的关系，再作分析”．
    丙说：“把字母a单独放在一边，再作分析”．
    参考上述思路，或自已的其它解法，可求出实数a的取值范围是    ．

    查看答案和解析>>


    同步练习册答案