题目列表(包括答案和解析)
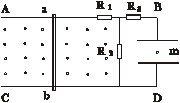
如图所示，两根足够长的平行金属导轨固定于同一水平面内，导轨间的距离为L，导轨上平行放置两根导体棒ab和cd，构成矩形回路。已知两根导体棒的质量均为m、电阻均为R，其它电阻忽略不计，整个导轨处于竖直向上的匀强磁场中，磁感应强度为B，导体棒均可沿导轨无摩擦的滑行。开始时，导体棒cd静止、ab有水平向右的初速度v0，两导体棒在运动中始终不接触。求：
（1）开始时，导体棒ab中电流的大小和方向；
（2）从开始到导体棒cd达到最大速度的过程中，矩形回路产生的焦耳热；
（3）当ab棒速度变为
v0时，cd棒加速度的大小。
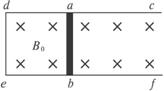
（1）若从t=0时刻起，磁感应强度均匀增加，每秒增量为K，同时保持棒静止，求棒中的感应电流的大小和方向。
（2）在上述（1）情况中，始终保持棒静止，当t=t1秒末时，需加的垂直于棒的水平拉力为多大？
（3）若从t=0时刻起，让金属棒ab以恒定速度v向左做匀速运动。要使棒ab到达ed之前棒中始终不产生感应电流，则磁感应强度应怎样随时间变化（写出B与t的关系式）？
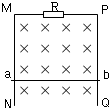如图所示，相距为L的两根竖直的足够长的光滑导轨MN、PQ，M、P之间接一阻值为R的定值电阻，金属棒ab质量为m，与导轨接触良好．整个装置处在方向垂直纸面向里水平匀强磁场中，金属棒和导轨电阻不计．现让ab棒由静止释放，经时间t达稳定状态，此时ab棒速度为v；
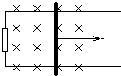如图，固定于水平地面上接有阻值为R=0.50Ω的电阻的光滑金属框架上放置一金属棒ab，金属框架宽度为L=1.0m，垂直于质量为m=1.0kg的金属棒ab施加一水平恒力F=1.0N，使棒从静止开始运动，当速度达到最大值时，电阻R上产生的焦耳热为Q=0.50J，整个装置处于竖直向下的匀强磁场中，磁感应强度为B=1.0T，金属棒的电阻为r=0.50Ω，不计其它电阻，求：选择题。共40分，1－5题只有一个选项正确，选对的得4分，选错或不答的得0分；6－10题，选对的得4分，选对但不全的得2分，有选错或不答的得0分。
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
D
C
B
AC
BC
AD
BD
BD
11．（9分）（1）
(3分) （2）2T0 (3分) （3）
（或
） (3分)
12．（11分）（1）电压表V2 (3分) （2）电阻R3＝20Ω (4分) （3）E＝6V (4分)
13．（14分）设汽车所受阻力与车所受重力的比例系数为k，则空载时汽车所受阻力为：
f0 = km
当汽车达到最大速度v0时，牵引力F0 = f0
可得汽车的额定功率P＝F0v0＝km0gv0……………………………………………………（4分）
同理，当汽车载货时：
P = k（m0＋m）gvm ………………………………………………………………………(4分)
解得：
……………………………………………………………………(4分)
14、（14分）他们的解法都不对。………………………………（4分）
设摩托车的加速时间为t，且正好用时t0＝3min追上汽车，则有：
……………………………………………………………（5分）
得 
…………………………………………………………………………（3分）
所以摩托车的最小加速度大小为 
m/s2 ……………………………（2分）
15．（15分）
⑴激光束a、b经过玻璃砖的折射光路图如图所示：……………………………………（4分）
如图，
得
…………………………………………………（2分）
激光束b，在O点有：
得
…………… ……………………（2分）
又 
得
激光束a，在C点有： 
得
在E点 
得
………………………………………（2分）
由
′，两束光射出后应平行，故不相交。
⑵在△CDO中，
在△CDE中，
在△EFO中，
……………………………（5分）
所以，光束a射出玻璃砖后与x轴交点的坐标为（
，0）
16．（15分）
⑴当金属棒ab和cd的速度相同时，对它们构成的系统，
F=ma＋2ma …………………………………………………………………………（2分）
得加速度 
………………………………………………………………………（3分）
⑵当金属棒ab的速度是金属棒cd的速度的2倍时，即 vab=2vcd
对金属棒ab，由牛顿第二定律得
…………………………………………………………（3分）
得 
………………………………………………（3分）
⑶对系统，由动量定理： 
………………………………………………（2分）
得： 
…………………………………………………………（2分）
17．（16分）
⑴如图，电荷从A点匀加速运动运动到x轴的C点的
过程：位移s＝AC＝
m
加速度 
＝
m/s2…（3分）
时间 
s ………………（2分）
⑵电荷到达C点的速度为
m/s ………………（2分）
速度方向与x轴正方向成45°角，在磁场中运动时
由 
得
m ………………………………………………（4分）
即电荷在磁场中的偏转半径为
m
⑶轨迹圆与x轴相交的弦长为
m，所以电荷从坐标原点O再次进入电场中，且速度方向与电场方向垂直，电荷在电场中作类平抛运动，运动过程中与x轴第三次相交时的位移方向角为45°，设运动的时间为t′，则：
间s=
得t′＝2×10－6s ………………………………………………………………（2分）
则s平=vt′=
m
m ……………………………………………………………（3分）
即电荷第三次到达x轴上的点的坐标为（8，0）
18．（16分）
⑴小球与滑块相互作用过程中沿水平方向动量守恒：
…………………………………………………………（3分）
又因为系统机械能守恒：
…………………………………（3分）
得 
…………………………………………（2分）
⑵当金属小球通过A点时，沿导轨方向金属小球与金属滑块具有共同速度v，沿A点切线方向的速度为v′，由动量和能量守恒得
………………………………………………………………（2分）
………………………………………………（2分）
解得
……………………………………………………（2分）
由牛顿第二定律得
………………………………………………（2分）
即为对金属块的作用力大小为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com