练习册

  • 练习册
  • 试题
    (II)求所得分数的分布列和数学期望. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题共13分）

         某公司要将一批海鲜用汽车运往A城，如果能按约定日期送到，则公司可获得销售收入30万元，每提前一天送到，或多获得1万元，每迟到一天送到，将少获得1万元，为保证海鲜新鲜，汽车只能在约定日期的前两天出发，且行驶路线只能选择公路1或公路2中的一条，运费由公司承担，其他信息如表所示.

        统计信息

    汽车行驶

    路线

    不堵车的情况下到达所需时间（天）

    堵车的情况下到达所需时间（天）

    堵车的概率

    运费（万元）

    公路1

    2

    3

    1.6

    公路2

    1

    4

    0.8

       （I）记汽车走公路1时公司获得的毛利润为（万元），求的分布列和数学期望

       （II）假设你是公司的决策者，你选择哪条公路运送海鲜有可能获得的毛利润更多？

    （注：毛利润=销售收入-运费）

    查看答案和解析>>

    （本小题共13分）

         某公司要将一批海鲜用汽车运往A城，如果能按约定日期送到，则公司可获得销售收入30万元，每提前一天送到，或多获得1万元，每迟到一天送到，将少获得1万元，为保证海鲜新鲜，汽车只能在约定日期的前两天出发，且行驶路线只能选择公路1或公路2中的一条，运费由公司承担，其他信息如表所示.

        统计信息

     

     

    汽车行驶

    路线

    不堵车的情况下到达所需时间（天）

    堵车的情况下到达所需时间（天）

    堵车的概率

    运费（万元）

    公路1

    2

    3

    1.6

    公路2

    1

    4

    0.8

       （I）记汽车走公路1时公司获得的毛利润为（万元），求的分布列和数学期望

       （II）假设你是公司的决策者，你选择哪条公路运送海鲜有可能获得的毛利润更多？

    （注：毛利润=销售收入-运费）

     

    查看答案和解析>>

    （本小题共13分）

            某公司要将一批海鲜用汽车运往A城，如果能按约定日期送到，则公司可获得销售收入30万元，每提前一天送到，或多获得1万元，每迟到一天送到，将少获得1万元，为保证海鲜新鲜，汽车只能在约定日期的前两天出发，且行驶路线只能选择公路1或公路2中的一条，运费由公司承担，其他信息如表所示.

        统计信息

    汽车行驶

    路线

    不堵车的情况下到达所需时间（天）

    堵车的情况下到达所需时间（天）

    堵车的概率

    运费（万元）

    公路1

    2

    3

    1.6

    公路2

    1

    4

    0.8

       （I）记汽车走公路1时公司获得的毛利润为（万元），求的分布列和数学期望

       （II）假设你是公司的决策者，你选择哪条公路运送海鲜有可能获得的毛利润更多？

    （注：毛利润=销售收入-运费）

    查看答案和解析>>

    （本小题共13分）

            某公司要将一批海鲜用汽车运往A城，如果能按约定日期送到，则公司可获得销售收入30万元，每提前一天送到，或多获得1万元，每迟到一天送到，将少获得1万元，为保证海鲜新鲜，汽车只能在约定日期的前两天出发，且行驶路线只能选择公路1或公路2中的一条，运费由公司承担，其他信息如表所示.

        统计信息

    汽车行驶

    路线

    不堵车的情况下到达所需时间（天）

    堵车的情况下到达所需时间（天）

    堵车的概率

    运费（万元）

    公路1

    2

    3

    1.6

    公路2

    1

    4

    0.8

       （I）记汽车走公路1时公司获得的毛利润为（万元），求的分布列和数学期望

       （II）假设你是公司的决策者，你选择哪条公路运送海鲜有可能获得的毛利润更多？

    （注：毛利润=销售收入-运费）

    查看答案和解析>>

    在某大学自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩为B的考生有10人.

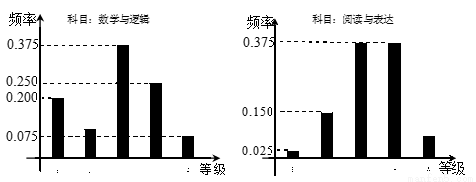
    （Ⅰ）求该考场考生中“阅读与表达”科目中成绩为A的人数；

    （Ⅱ）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分.

    （i）求该考场考生“数学与逻辑”科目的平均分；

    (ii)若该考场共有10人得分大于7分，其中有2人10分，2人9分，6人8分. 从这10

    人中随机抽取两人，求两人成绩之和的分布列和数学期望.

     

    查看答案和解析>>

    一、选择题

    1、B      

    2、A    

    3、D  ④少了“”这个条件，其余3个是正确的。

    4、B      

    5、C  取AC的中点O，则  四面体ABCD外接球的球心为O，半径为 

    6、D  设

    7、D  由题意知，P点的轨迹为抛物线，以AB的中点为原点，AB所在直线为轴或轴可得四个标准方程

    8、A 

    9、A  ，1，－1是方程的两根

    10、C  若无最小值

    当  有最小值等价于

    有大于0的最小值，即

    11、C      

      直线AB的斜率为1

    当过C点的切线与AB平行时，面积取最大值设此直线方程为

        

      C到AB距离为

    12、C  的整数解为

    这8个点两两所连的不过原点的直线有24条，过这8个点的切线有8条，每条直线确定了唯一的有序数对,共有32条。

    二、填空题

    13、 

     

    14、    取AD中点E，连  为菱形，且

    在侧面

    上的投影，为所求，

    15、 0  

    又为偶函数 

    16、 ②④   ①错  ②对

     ③错 

     当且仅当取等号  ④对

    三、解答题

    17、（1）

      即时 有最大值

    （2）

    18、（1）该爱好者得2分的概率为

    （2）答对题的个数为，得分为，的可能取值为0，2，4，8

     

      

    的分布列为

    0

    2

    4

    8

    P

    的数学期望为

    以D为原点，DA、DC、DP分别为轴建系如图，

    则

    19、（1）       

    由  知为平面PAD的一个法向量

    又    

    （2） 

    （3）由（1）知为平面的一个法向量，

    设平面的法向量为

    令

     即二面角的余弦值为

    20、（1）

     当   当

    上单增

    处取得极小值

        

    的最大值为  最小值为

    （2）由（1）知当

    故对任意

    只要对任意恒成立，即恒成立

    记    

    实数的取值范围是

    21、（1）

      当

    不是等比数列，当时， 数列是等比数列

    且公比为2，

    （2）由（1）知当

     1°

      2°

    1°－2°及－

                  

                  

    即

    22、（1）设椭圆C的方程为

    椭圆C的方程为

    （2）由

      设与椭圆C交点为

    将

    ①

    则

    消去得 

    即    

      由①得

        

    综上所述

     


    同步练习册答案