
题目列表(包括答案和解析)
设函数![]() 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{![]() }满足
}满足![]() .证明:数列{
.证明:数列{![]() }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有![]() 成立.
成立.
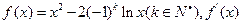 表示f(x)导函数。
表示f(x)导函数。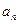 }满足
}满足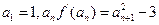 .证明:数列{
.证明:数列{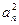 }中
}中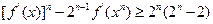 成立.
成立.(09年潍坊一模文)(14分)
设函数![]() 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{![]() }满足
}满足![]() .证明:数列{
.证明:数列{![]() }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有![]() 成立.
成立.
设函数f(x)=x2-2(-1)klnx(k∈N*),![]() 表示f(x)导函数.
表示f(x)导函数.
(Ⅰ)求函数一份(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,![]() .证明:数列{an2}中不存在成等差数列的三项;
.证明:数列{an2}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,设![]() ,数列{bn}的前n项和为Sn,证明不等式
,数列{bn}的前n项和为Sn,证明不等式![]() 对一切正整数n均成立,并比较S2009-1与ln2009的大小.
对一切正整数n均成立,并比较S2009-1与ln2009的大小.
设函数f(x)=x2-2(-1)klnx(k∈N*),![]() (x)表示f(x)导函数.
(x)表示f(x)导函数.
(Ⅰ)求函数一份(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,an![]() (an)=
(an)=![]() -3.证明:数列{
-3.证明:数列{![]() }中不存在成等差数列的三项;
}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,设bn=![]() (n)-n,数列{bn}的前n项和为Sn,证明不等式
(n)-n,数列{bn}的前n项和为Sn,证明不等式![]() 对一切正整数n均成立,并比较S2009-1与In2009的大小.
对一切正整数n均成立,并比较S2009-1与In2009的大小.
.files\image156.jpg)
.files\image158.jpg)
.files\image160.jpg)
.files\image162.jpg)
.files\image164.jpg)
.files\image166.jpg)
.files\image168.jpg)
.files\image170.jpg)
.files\image172.jpg)
.files\image174.jpg)
.files\image176.jpg)
.files\image178.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com