
题目列表(包括答案和解析)
(2005
辽宁,17)如下图,已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.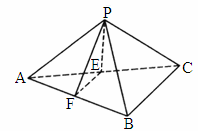
(1)
证明:PC⊥平面PAB;(2)
求二面角P—AB—C的平面角的余弦值;(3)
若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得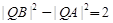 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: 为定值.
为定值.
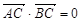 ,|BC|=2|AC|.
,|BC|=2|AC|.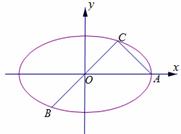
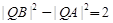 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.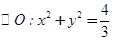 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: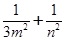 为定值.
为定值.1.解:依题设有:.files/image517.gif) ………………………………………4分
………………………………………4分
令.files/image519.gif) ,则
,则.files/image521.gif) …………………………………………5分
…………………………………………5分
.files/image523.gif) …………………………………………7分
…………………………………………7分
.files/image521.gif)
.files/image525.gif)
.files/image527.gif)
.files/image527.gif)
.files/image530.gif) ………………………………10分
………………………………10分
2.解:以有点为原点,极轴为.files/image532.gif) 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1).files/image534.gif) ,
,.files/image536.gif) ,由
,由.files/image538.gif) 得
得.files/image540.gif) .
.
所以.files/image542.gif) .
.
即.files/image544.gif) 为圆
为圆.files/image285.gif) 的直角坐标方程. ……………………………………3分
的直角坐标方程. ……………………………………3分
同理.files/image547.gif) 为圆
为圆.files/image287.gif) 的直角坐标方程. ……………………………………6分
的直角坐标方程. ……………………………………6分
(2)由.files/image550.gif)
相减得过交点的直线的直角坐标方程为.files/image552.gif) . …………………………10分
. …………………………10分
3.(必做题)(本小题满分10分)
解:(1)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的.files/image035.gif) , 则其概率为
, 则其概率为.files/image555.gif) …………………………………………4分
…………………………………………4分
答:恰好选到1个曾经参加过数学研究性学习活动的同学的概率为.files/image557.gif)
(2)随机变量.files/image559.gif)
.files/image561.gif) ……………………5分
……………………5分
.files/image563.gif) …………………………6分
…………………………6分
.files/image565.gif) ………………………………7分
………………………………7分
∴随机变量.files/image291.gif) 的分布列为
的分布列为
.files/image291.gif)
2
3
4
P
.files/image569.gif)
.files/image571.gif)
.files/image573.gif)
∴.files/image575.gif) …………………………10分
…………………………10分
4.(必做题)(本小题满分10分)
(1).files/image577.gif) ,
,.files/image579.gif) ,
,.files/image581.gif) ,
,.files/image583.gif)
.files/image585.gif) ,
,.files/image587.gif)
.files/image589.gif) ……………………………………3分
……………………………………3分
(2)平面BDD1的一个法向量为.files/image591.gif)
设平面BFC1的法向量为.files/image593.gif)
.files/image595.gif) ∴
∴.files/image597.gif)
取.files/image599.gif) 得平面BFC1的一个法向量
得平面BFC1的一个法向量.files/image601.gif)
.files/image603.gif) ∴所求的余弦值为
∴所求的余弦值为.files/image605.gif) ……6分
……6分
(3)设.files/image607.gif) (
(.files/image609.gif) )
)
.files/image611.gif) ,由
,由.files/image613.gif) 得
得.files/image615.gif)
即.files/image617.gif) ,
,.files/image619.gif)
.files/image621.gif)
.files/image623.gif)
.files/image625.gif)
.files/image343.gif) 当
当.files/image628.gif) 时,
时,.files/image630.gif)
当.files/image632.gif) 时,∴
时,∴.files/image634.gif) ……………………………………10分
……………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com