
题目列表(包括答案和解析)
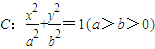 的离心率为
的离心率为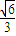 ,右准线方程为
,右准线方程为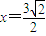 ,左、右焦点分别为F1,F2.
,左、右焦点分别为F1,F2.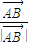 在向量
在向量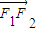 方向上的投影是p,且
方向上的投影是p,且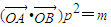 (O为坐标原点),求m与k的关系式;
(O为坐标原点),求m与k的关系式;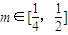 时,求△ABC面积的取值范围.
时,求△ABC面积的取值范围.已知椭圆![]() 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证:![]()
已知椭圆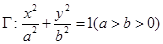 的离心率为
的离心率为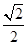 ,且椭圆
,且椭圆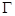 的右焦点
的右焦点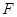 与抛物线
与抛物线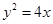 的焦点重合.
的焦点重合.
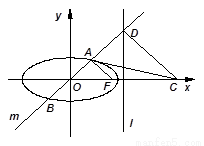
(Ⅰ)求椭圆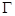 的标准方程;
的标准方程;
(Ⅱ)如图,设直线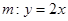 与椭圆
与椭圆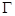 交于
交于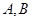 两点(其中点
两点(其中点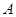 在第一象限),且直线
在第一象限),且直线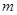 与定直线
与定直线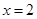 交于点
交于点 ,过
,过 作直线
作直线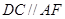 交
交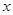 轴于点
轴于点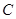 ,试判断直线
,试判断直线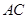 与椭圆
与椭圆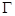 的公共点个数.
的公共点个数.
已知椭圆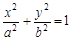
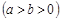 的离心率为
的离心率为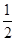 ,两焦点之间的距离为4.
,两焦点之间的距离为4.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右顶点作直线交抛物线 于A、B两点,
于A、B两点,
(1)求证:OA⊥OB;
(2)设OA、OB分别与椭圆相交于点D、E,过原点O作直线DE的垂线OM,垂足为M,证明|OM|为定值.
已知椭圆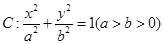 的离心率为
的离心率为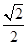 ,且过点
,且过点 ,过
,过 的右焦点
的右焦点 任作直线
任作直线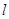 ,设
,设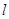 交
交 于
于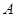 ,
,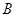 两点(异于
两点(异于 的左、右顶点),再分别过点
的左、右顶点),再分别过点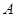 ,
,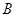 作
作 的切线
的切线 ,
, ,记
,记 与
与 相交于点
相交于点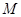 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)证明:点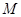 在一条定直线上.
在一条定直线上.

一、选择题(每小题5 分,共40 分)
DCABD ABC
二、填空题(每小题5 分,共35分)
9. 10.
10. 11.91
12.②④
11.91
12.②④
13. 14.(i)
14.(i) (2分) (ii)
(2分) (ii) (3分)
(3分)
15.(i) (3分); (ii)
(3分); (ii) (2分)
(2分)
|