
题目列表(包括答案和解析)
| 1 | 2 |
| a |
| 2 |
| b |
| 2 |
| x-1 |
若函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且在
上的奇函数,且在![]() 上单调递增,若实数
上单调递增,若实数![]() 满足:
满足:![]() ,求
,求![]() 的取值范围. ( )
的取值范围. ( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
若函数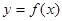 是定义在区间
是定义在区间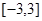 上的奇函数,且在
上的奇函数,且在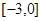 上单调递增,若
上单调递增,若
实数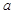 满足:
满足: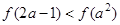 ,求
,求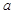 的取值范围.
的取值范围.
若函数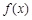 为定义域
为定义域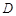 上单调函数,且存在区间
上单调函数,且存在区间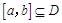 (其中
(其中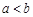 ),使得当
),使得当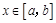 时,
时,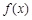 的取值范围恰为
的取值范围恰为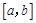 ,则称函数
,则称函数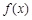 是
是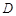 上的正函数,区间
上的正函数,区间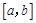 叫做等域区间.
叫做等域区间.
(1)已知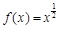 是
是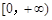 上的正函数,求
上的正函数,求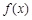 的等域区间;
的等域区间;
(2)试探究是否存在实数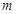 ,使得函数
,使得函数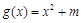 是
是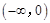 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数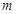 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
三.解答题:
17.解:记“甲回答对这道题”、“ 乙回答对这道题”、“丙回答对这道题”分别为事件卷.files/image032.gif) 、
、卷.files/image034.gif) 、
、卷.files/image036.gif) ,则
,则卷.files/image348.gif) ,且有
,且有卷.files/image350.gif) ,即
,即卷.files/image352.gif)
则甲、乙、丙三人中恰有两人回答对该题的概率为:
18. 解法一 公理化法
(1)当卷.files/image362.gif) 时,取
时,取卷.files/image170.gif) 的中点
的中点卷.files/image365.gif) ,连接
,连接卷.files/image367.gif) ,因为
,因为卷.files/image139.gif) 为正三角形,则
为正三角形,则卷.files/image370.gif) ,由于
,由于卷.files/image209.gif) 为
为卷.files/image373.gif) 的中点时,
的中点时,卷.files/image375.gif)
卷.files/image385.gif) ∵
∵卷.files/image387.gif) 平面
平面卷.files/image389.gif) ,∴
,∴卷.files/image391.gif) 平面
平面卷.files/image389.gif) ,∴
,∴卷.files/image394.gif) .………………………………………………4分
.………………………………………………4分
(2)当卷.files/image217.gif) 时,过
时,过卷.files/image209.gif) 作
作卷.files/image398.gif) 于
于卷.files/image400.gif) ,如图所示,则
,如图所示,则卷.files/image402.gif) 底面
底面卷.files/image095.gif) ,过
,过卷.files/image400.gif) 作
作卷.files/image406.gif) 于
于卷.files/image408.gif) ,连结
,连结卷.files/image410.gif) ,则
,则卷.files/image412.gif) ,
,卷.files/image414.gif) 为二面角
为二面角卷.files/image219.gif) 的平面角,
的平面角,
卷.files/image429.gif) ,即二面角
,即二面角卷.files/image219.gif) 的大小为
的大小为卷.files/image431.gif) .…………………………………………………8分
.…………………………………………………8分
即卷.files/image221.gif) 到平面
到平面卷.files/image223.gif) 的距离为
的距离为卷.files/image455.gif) .…………………………………………………………………………12分
.…………………………………………………………………………12分
解法二 向量法
以卷.files/image032.gif) 为原点,
为原点,卷.files/image170.gif) 为
为卷.files/image109.gif) 轴,过
轴,过卷.files/image032.gif) 点与
点与卷.files/image170.gif) 垂直的直线为
垂直的直线为卷.files/image159.gif) 轴,
轴,卷.files/image461.gif) 为
为卷.files/image463.gif) 轴,建立空间直角坐标系
轴,建立空间直角坐标系卷.files/image465.gif) ,如图所示,
,如图所示,
又由于二面角卷.files/image219.gif) 是一个锐角,则二面角
是一个锐角,则二面角卷.files/image219.gif) 的大小是
的大小是卷.files/image431.gif) .……………………8分
.……………………8分
卷.files/image508.gif)
卷.files/image221.gif) 到平面
到平面卷.files/image223.gif) 的距离为
的距离为卷.files/image455.gif) .………………………………………………………………………12分
.………………………………………………………………………12分
卷.files/image508.gif) 实数
实数卷.files/image235.gif) 的取值范围是
的取值范围是卷.files/image557.gif) .………………………………………………………12分
.………………………………………………………12分
则直线卷.files/image257.gif) 的方程是
的方程是卷.files/image595.gif) ,则直线
,则直线卷.files/image257.gif) 过定点
过定点卷.files/image597.gif) .………………………………………8分
.………………………………………8分
而卷.files/image032.gif) 到直线
到直线卷.files/image257.gif) 的距离
的距离卷.files/image601.gif) ,当且仅当
,当且仅当卷.files/image603.gif) 即
即卷.files/image605.gif) 时取等号.………………………………………………………………10分
时取等号.………………………………………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com