
题目列表(包括答案和解析)
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、班级和考号填写在答题卷上。
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
|
运输工具 |
运输费单价:元/(吨?千米) |
冷藏费单价:元/(吨?时) |
固定费用:元/次 |
|
汽车 |
2 |
5 |
200 |
|
火车 |
1.6 |
5 |
2280 |


(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为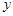 汽(元)和
汽(元)和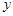 火(元),分别求
火(元),分别求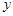 汽、
汽、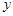 火与
火与  的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时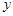 汽>
汽>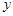 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
第Ⅰ卷 选择题(共50分)
一、选择题(本大题共10小题,每小题5分,满分50分)
 1、设全集U={
1、设全集U={![]() 是不大于9的正整数},
是不大于9的正整数},![]() {1,2,3 },
{1,2,3 },![]() {3,4,5,6}则图中阴影部分所表示的集合为( )
{3,4,5,6}则图中阴影部分所表示的集合为( )
A.{1,2,3,4,5,6} B. {7,8,9}
C.{7,8} D. {1,2,4,5,6,7,8,9}
2、计算复数(1-i)2-![]() 等于( )
等于( )
A.0 B.2 C. 4i D. -4i
| 2 | 3 |
一. 选择题(本大题共8小题,每小题5分,共40分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
A
B
A
D
D
B
C
C
二. 填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9) .files\image229.gif) (10)
(10) .files\image231.gif) (11)
(11) .files\image233.gif) 或
或.files\image235.gif) (12)
(12) .files\image237.gif) (13)
(13) .files\image239.gif) ,
,.files\image241.gif)
(14) 10,
.files\image243.gif)
三.解答题 (本大题共6小题,共80分)
(15) (共12分)
解:(I).files\image245.gif)
.files\image129.gif) ,
,.files\image131.gif) ,
,
.files\image247.gif)
.files\image125.gif)
.files\image127.gif) =
=.files\image249.gif) ?
?.files\image251.gif)
.files\image253.gif) ------------------2分
------------------2分
.files\image255.gif) ------------------4分
------------------4分
.files\image256.gif)
.files\image135.gif) =
= .files\image258.gif) .
------------------5分
.
------------------5分
又.files\image137.gif)
.files\image261.gif)
.files\image263.gif) -----------------6分
-----------------6分
.files\image256.gif) 函数
函数.files\image137.gif) 的最大值为
的最大值为.files\image265.gif) .
------------------7分
.
------------------7分
当且仅当.files\image267.gif) (
(.files\image269.gif) Z)时,函数
Z)时,函数.files\image137.gif) 取得最大值为
取得最大值为.files\image265.gif) .
.
(II)由.files\image271.gif) (
(.files\image269.gif) Z),
------------------9分
Z),
------------------9分
得.files\image273.gif) ,
------------------11分
,
------------------11分
.files\image256.gif) 函数
函数.files\image137.gif) 的单调递增区间为[
的单调递增区间为[.files\image275.gif) ](
](.files\image269.gif) Z). ------------------12分
Z). ------------------12分
(16) (共14分)
解法一:
解:(Ⅰ).files\image278.gif) 且
且.files\image280.gif) 平面
平面.files\image282.gif) .--------------------2分
.--------------------2分
.files\image284.gif) 为
为.files\image286.gif) 在平面
在平面.files\image282.gif) 内的射影.
--------------------3分
内的射影.
--------------------3分
又.files\image289.gif) ⊥
⊥.files\image149.gif) , ∴
, ∴.files\image149.gif) ⊥
⊥.files\image147.gif) .
--------------------4分
.
--------------------4分
(Ⅱ) 由(Ⅰ).files\image149.gif) ⊥
⊥.files\image147.gif) ,又
,又.files\image149.gif) ⊥
⊥.files\image289.gif) ,
,
∴.files\image296.gif) 为所求二面角的平面角.
--------------------6分
为所求二面角的平面角.
--------------------6分
又∵.files\image298.gif) =
=.files\image300.gif)
.files\image149.gif) =4,
=4,
∴.files\image147.gif) =4 . ∵
=4 . ∵.files\image289.gif) =2 , ∴
=2 , ∴.files\image296.gif) =60°.
--------------------9分
=60°.
--------------------9分
.files\image302.gif) 即二面角
即二面角.files\image151.gif) 大小为60°.
大小为60°.
(Ⅲ)过.files\image304.gif) 作
作.files\image306.gif) 于D,连结
于D,连结.files\image308.gif) ,
,
由(Ⅱ)得平面.files\image310.gif) 平面
平面.files\image312.gif) ,又
,又.files\image314.gif)
.files\image316.gif) 平面
平面.files\image318.gif) ,
,
∴平面.files\image312.gif)
.files\image320.gif) 平面
平面.files\image318.gif) ,且平面
,且平面.files\image312.gif)
.files\image322.gif) 平面
平面.files\image324.gif) ,
,
∴.files\image326.gif) 平面
平面.files\image318.gif) .
.
∴.files\image328.gif) 为
为.files\image153.gif) 在平面
在平面.files\image318.gif) 内的射影.
内的射影.
.files\image331.gif) . -----------------11分
. -----------------11分
在.files\image333.gif) 中,
中,.files\image335.gif) ,
,
在.files\image337.gif) 中,
中,.files\image339.gif) ,
,.files\image341.gif) .
.
∴.files\image343.gif) =
=.files\image345.gif) .
-------------------13分
.
-------------------13分
所以直线.files\image347.gif) 与平面
与平面.files\image155.gif) 所成角的大小为
所成角的大小为.files\image349.gif) .
-------------------14分
.
-------------------14分
解法二:
解:(Ⅰ)由已知.files\image142.gif) ,
,
以.files\image062.gif) 点为原点,建立如图所示的空间直角坐标系
点为原点,建立如图所示的空间直角坐标系.files\image352.gif) .
.
则 .files\image354.gif) ,
,.files\image356.gif) .
-------------------2分
.
-------------------2分
则.files\image358.gif) ,
,.files\image360.gif) .
.
.files\image362.gif)
.files\image364.gif) .
.
.files\image366.gif) .
-------------------4分
.
-------------------4分
(Ⅱ).files\image368.gif) ,
,.files\image370.gif) 平面
平面.files\image282.gif) .
.
.files\image373.gif) 是平面
是平面.files\image282.gif) 的法向量. -------------------5分
的法向量. -------------------5分
设侧面.files\image318.gif) 的法向量为
的法向量为.files\image377.gif)
.files\image379.gif) ,
,
.files\image358.gif) ,
,.files\image360.gif) .
.
.files\image381.gif) ,
,
.files\image383.gif)
.files\image385.gif) .令
.令.files\image387.gif) 则
则.files\image389.gif) .
.
则得平面.files\image318.gif) 的一个法向量
的一个法向量.files\image377.gif)
.files\image392.gif) . -------------------7分
. -------------------7分
.files\image394.gif) .
-------------------8分
.
-------------------8分
即二面角.files\image151.gif) 大小为60°.
-------------------9分
大小为60°.
-------------------9分
(Ⅲ)由(II)可知.files\image377.gif)
.files\image392.gif) 是平面
是平面.files\image318.gif) 的一个法向量.
-------------------10分
的一个法向量.
-------------------10分
又.files\image399.gif) ,
, .files\image247.gif)
.files\image402.gif) .
-------------------13分
.
-------------------13分
所以直线.files\image153.gif) 与平面
与平面.files\image155.gif) 所成角为
所成角为.files\image406.gif) .
-------------------14分
.
-------------------14分
(17)(共13分)
解:(I)设乙闯关成功的概率为.files\image408.gif) ,丙闯关成功的概率为
,丙闯关成功的概率为.files\image410.gif) -------------------1分
-------------------1分
因为乙丙独立闯关,根据独立事件同时发生的概率公式得:
.files\image412.gif) -------------------3分
-------------------3分
解得.files\image414.gif) .
-------------------5分
.
-------------------5分
答:乙闯关成功的概率为.files\image416.gif) ,丙闯关成功的概率为
,丙闯关成功的概率为.files\image418.gif) .
.
(II)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A, -------------------6分
则.files\image420.gif) -------------------9分
-------------------9分
答:团体总分为4分的概率为.files\image422.gif) .
.
(III)团体总分不小于4分, 即团体总分为4分或6分,
设“团体总分不小于4分”为事件B, -------------------10分
由(II)知团体总分为4分的概率为.files\image422.gif) ,
,
团体总分为6分, 即3人都闯关成功的概率为.files\image424.gif) ------------------- 12分
------------------- 12分
所以参加复赛的概率为.files\image426.gif) =
=.files\image428.gif) -------------------13分
-------------------13分
答:该小组参加复赛的概率为.files\image430.gif) .
.
(18) (共13分)
解:(Ⅰ)第5行第5个数是29. ……………2分
(II) 由.files\image168.gif) 得
得.files\image433.gif) .
……………3分
.
……………3分
设.files\image435.gif) 是数列
是数列.files\image111.gif) 的前
的前.files\image437.gif) 项和, ∴
项和, ∴.files\image439.gif) .
.
当.files\image441.gif) 时,
时,.files\image443.gif) ……………5分
……………5分
当.files\image445.gif) 时,
时,.files\image447.gif) ……………6分
……………6分
又当.files\image441.gif) 时,
时,.files\image449.gif) ,
,
∴.files\image451.gif) ……………8分
……………8分
即数列.files\image111.gif) 的通项公式是
的通项公式是.files\image453.gif)
(III)由 (II)知数列.files\image111.gif) 是首项为1,公差为2的等差数列.
…………… 9分
是首项为1,公差为2的等差数列.
…………… 9分
∵前.files\image455.gif) 行共有项
行共有项.files\image457.gif)
∴第.files\image050.gif) 行的第一项为
行的第一项为.files\image460.gif) ………… 11分
………… 11分
∴第.files\image050.gif) 行构成首项为
行构成首项为.files\image463.gif) ,公差为2的等差数列,且有
,公差为2的等差数列,且有.files\image050.gif) 项.
项.
∴.files\image466.gif) .
……………13分
.
……………13分
(19)(共14分)
解:(I)设点.files\image468.gif) , 由已知得点
, 由已知得点.files\image191.gif) 在
在.files\image471.gif) 的中垂线上,
-------------------1分
的中垂线上,
-------------------1分
即.files\image473.gif) ,
------------------2分
,
------------------2分
根据抛物线的定义知,动点.files\image191.gif) 在以F为焦点,以直线m为准线的抛物线上, ------------------4分
在以F为焦点,以直线m为准线的抛物线上, ------------------4分
∴点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com