
题目列表(包括答案和解析)
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
在等差数列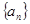 中,
中,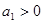 ,
,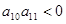 ,若此数列的前10项和
,若此数列的前10项和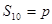 ,前18项和
,前18项和 ,则数列
,则数列 的前18项和
的前18项和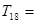 ___________.
___________.
在等差数列{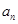 }中,
}中,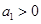 ,
,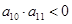 ,若此数列的前10项和
,若此数列的前10项和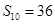 ,前18项和
,前18项和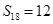 ,则数列{
,则数列{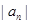 }的前18项和
}的前18项和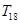 的值是( )
的值是( )
A.24 B.48 C.60 D.84
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
B
C
D
A
D
C
C
D
B
二、填空题(每小题5分,共20分)
13、(1,2); 14、20; 15、21;16、 .
.
三、解答题
17、解:(Ⅰ)当 时,有
时,有 ,又
,又 ,所以
,所以 ……1分
……1分
当 时,
时,
=

所以 ,且当
,且当 时,
时, ……3分
……3分
又 ,因此数列{
,因此数列{ }是以1为首项
}是以1为首项
且公差为2的等差数列,所以 ……2分
……2分
(Ⅱ)证明:(1)当 时,
时, ,
, ,关系成立
……1分
,关系成立
……1分
(2)假设当 时,关系成立,即
时,关系成立,即 ,则
,则
……1分 那么
 ,即当
,即当 时关系也成立
时关系也成立
……3分 根据(1)和(2)知,关系式 对任意
对任意 N*都成立 ……1分
N*都成立 ……1分
 18、解:(Ⅰ)如图,以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则
18、解:(Ⅰ)如图,以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则 ,
, ,
, ,
,
 ,
, ,
, ……1分
……1分
设 ,则
,则 ,
, ,
,
即AM⊥BC,又因为 ,且
,且 ,
,
所以 AM^平面 ……3分
……3分
(Ⅱ) ,因为
,因为 ,所以
,所以 ,得
,得 ,
,
即 ,可得平面
,可得平面 的一个法向量为
的一个法向量为 =
= ……3分
……3分
 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,
则 且
且 ,得
,得 ,
, ,令
,令 ,得平面
,得平面 的一个法向量为
的一个法向量为 =
= ……3分设平面ABM与平面AB
……3分设平面ABM与平面AB ,
,
则 ……2分
……2分
19、解:(Ⅰ)随机变量甲、乙两名运动员选择的泳道相隔数X的分布列为:
X
0
1
2
3
4
5
6








……6分
泳道相隔数X的期望为:
E(X)= ……2分
……2分
(Ⅱ) ……4分
……4分
20、解:(Ⅰ)由 得
得 ……2分
……2分
可得直线 的方程为
的方程为 ,于是
,于是 ,
,
得 ,
, ,
, ,所以椭圆
,所以椭圆 的方程为
的方程为 ……2分
……2分
(Ⅱ)设 ,由方程组
,由方程组 得
得 ,
,
所以有 ,
, ,且
,且 ,即
,即 ……2分
……2分

 ……2分
……2分
因为 ,所以
,所以 ,又
,又 ,所以
,所以 是线段
是线段 的中点,
的中点,
点 的坐标为
的坐标为 ,即
,即 的坐标是
的坐标是 ,因此
,因此
直线 的方程为
的方程为 ,得点
,得点 的坐标为(0,
的坐标为(0, ),
),
所以 ……2分
……2分
因此
所以当 ,即
,即 时,
时, 取得最大值,最大值为
取得最大值,最大值为 ……2分
……2分
21、解:(Ⅰ)

 ……2分
……2分
若 ,则
,则 ,
, 为R上的单调递增函数;
为R上的单调递增函数;
若 ,
, 的解为
的解为 或
或 ,
, 的解为
的解为 ,
,
此时 在区间
在区间 单调递增,在区间
单调递增,在区间 单调递减;
单调递减;
若 ,
, 的解为
的解为 或
或 ,
, 的解为
的解为 ,
,
此时 在区间
在区间 单调递增,在区间
单调递增,在区间 单调递减……3分
单调递减……3分
(Ⅱ)当 时,
时, ,
, ,
,
因为 ,所以点
,所以点 (0,
(0, )不在曲线
)不在曲线 上,设过点
上,设过点 的直线与曲线
的直线与曲线 相切于点
相切于点 ,则切线方程为
,则切线方程为 ,所以有
,所以有 及
及
 ,得
,得 ……2分 令
……2分 令 ,
,
则 ,
,
令 ,得
,得 ,
, ,
, ,可得
,可得 在区间
在区间 单调递增,在区间
单调递增,在区间 单调递减,所以
单调递减,所以 在
在 时取极大值
时取极大值 ,
,
在 时取极小值
时取极小值 ,在
,在 时取极大值
时取极大值 ,又
,又 ,
,
 所以
所以 是
是 的最大值
……3分
的最大值
……3分
如图,过点 (0,
(0, )有且只有一条直线与曲线
)有且只有一条直线与曲线
相切等价于直线 与曲线
与曲线
有且只有一个交点,又当 时,
时, ,所以
,所以 或
或 ……2分
……2分
 22、(Ⅰ)证明:因为AB为⊙O直径,
22、(Ⅰ)证明:因为AB为⊙O直径,
所以 ∠ACB=90°,即 AC⊥BC,
因为D是弧 的中点,由垂径定理
的中点,由垂径定理
得OD⊥BC,因此OD∥AC ……3分
又因为点O为AB的中点,所以点E为
BC的中点,所以OE= AC ……2分
AC ……2分
(Ⅱ)证明:连结CD,因为PC是⊙O的切线,所以∠PCD=∠CAP,又∠P是公共角,所以 △PCD∽△PAC.得

 ,得
,得 ……3分
……3分
因为D是弧 的中点,所以
的中点,所以 ,因此
,因此 ……2分
……2分
23、解:(Ⅰ)曲线 上的动点
上的动点 的坐标为(
的坐标为( ,
, ),坐标原点
),坐标原点 (0,0),
(0,0),
设P的坐标为( ,
, ),则由中点坐标公式得
),则由中点坐标公式得 ,
, ,所以点P 的坐标为(
,所以点P 的坐标为( ,
, )……3分
)……3分
因此点 的轨迹的参数方程为
的轨迹的参数方程为 (
( 为参数,且
为参数,且 ),
),
消去参数 得点
得点 轨迹的直角坐标方程为
轨迹的直角坐标方程为 ……2分
……2分
(Ⅱ)由直角坐标与极坐标关系 得直线
得直线 的直角坐标方程为
的直角坐标方程为
 ……2分 又由(Ⅰ)知点
……2分 又由(Ⅰ)知点 的轨迹为圆心在原点半径为2的圆,
的轨迹为圆心在原点半径为2的圆,
因为原点(0,0)到直线 的距离为
的距离为
所以点 到直线
到直线 距离的最大值
距离的最大值 ……3分
……3分
24、解:(Ⅰ)由题意得 ,即
,即 得
得 ……2分
……2分
因为
所以 的取值范围是[0,6] ……3分
的取值范围是[0,6] ……3分
(Ⅱ) ,
,
因为对于 ,由绝对值的三角不等式得
,由绝对值的三角不等式得

 ……3分
……3分
于是有 ,得
,得 ,即
,即 的取值范围是
的取值范围是 ……2分
……2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com