
题目列表(包括答案和解析)
如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
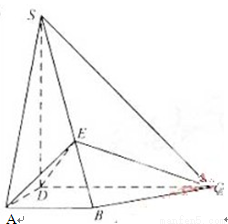
【解析】本试题主要考查了立体几何中的运用。
(1)证明:因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.,因此可知得到平面EDC⊥平面SBC.
(Ⅱ)由SA2= SD2+AD2 = 5 ,AB=1,SE=2EB,AB⊥SA,知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
取ED中点F,连接AF,则AF⊥DE,AF2= AD2-DF2 =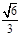 .
.
连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG= 2 ,FG2= DG2-DF2
=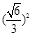 ,
,
cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ,
所以,二面角A-DE-C的大小为120°
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
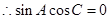

又由 得
得 即
即

又由 得
得 即
即

又
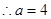 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

如图,在南北方向直线延伸湖岸上有一港口A,一汽艇以60 km/h的速度从A出发,30分钟后因故障而停在湖里.已知汽艇出发后按直线前进,以后又改成正东方向航行,但不知最初的方向和何时改变方向.现要去营救,请用图表示营救的区域.

在△ABC中,角A、B、C的对边分别为a、b、c,向量 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
=
(Ⅰ)求角B的大小;
(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
【解析】本试题主要考查了向量的数量积和三角函数,以及解三角形的综合运用
第一问中由条件|p +q |=| p -q |,两边平方得p·q=0,又
p=(sinA,b+c),q=(a-c,sinC-sinB),代入得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,
即 ,又由余弦定理
,又由余弦定理 =2acosB,所以cosB=
=2acosB,所以cosB= ,B=
,B=
第二问中,m=(sin(C+ ),
), ),n=(2k,cos2A) (k>1),m·n=2ksin(C+
),n=(2k,cos2A) (k>1),m·n=2ksin(C+ )+
)+ cos2A=2ksin(C+B) +
cos2A=2ksin(C+B) + cos2A
cos2A
=2ksinA+ -
- =-
=- +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).
(k>1).
而0<A< ,sinA∈(0,1],故当sin=1时,m·n取最大值为2k-
,sinA∈(0,1],故当sin=1时,m·n取最大值为2k- =3,得k=
=3,得k= .
.
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列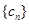 的前
的前 项和
项和 .
.
【解析】第一问利用由 得
得
两式相减得
故 时,
时,
从而 又
又 即
即 ,而
,而
从而 故
故
第二问中,
 又
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为
第三问中,
 两边同乘以
两边同乘以
利用错位相减法得到和。
(1)由 得
得
两式相减得
故 时,
时,
从而 ………………3分
………………3分
又 即
即 ,而
,而
从而 故
故
 对任意
对任意 ,
, 为常数,即
为常数,即 为等比数列………………5分
为等比数列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为 ………………9分
………………9分
(3)
 两边同乘以
两边同乘以
 ………………11分
………………11分
两式相减得

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com