阅读下列材料：

正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．

数学老师给小明同学出了一道题目：在图正方形网格（每个小正方形边长为1）中画出格点△ABC，使，；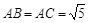

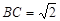小明同学的做法是：由勾股定理，得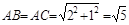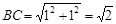，，于是画出线段AB、AC、BC，从而画出格点△ABC．

（1）请你参考小明同学的做法，在图中的正方形网格（每个小正方形边长为1）中画出格点△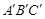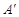（点位置如图所示），使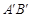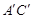＝＝5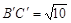，．（直接画出图形，不写过程）；

（2）观察△ABC与△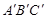的形状，猜想∠BAC与∠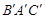有怎样的数量关系，并证明你的猜想．

阅读下列材料：
正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．
数学老师给小明同学出了一道题目：在图正方形网格（每个小正方形边长为1）中画出格点△ABC，使，；
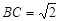小明同学的做法是：由勾股定理，得，，于是画出线段AB、AC、BC，从而画出格点△ABC．
（1）请你参考小明同学的做法，在图中的正方形网格（每个小正方形边长为1）中画出格点△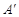（点位置如图所示），使＝＝5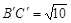，．（直接画出图形，不写过程）；
（2）观察△ABC与△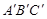的形状，猜想∠BAC与∠有怎样的数量关系，并证明你的猜想．
      

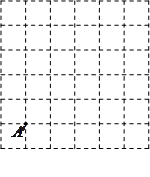
解：（1）如图①AH=AB

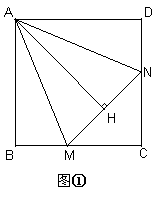（2）数量关系成立.如图②，延长CB至E，使BE=DN

∵ABCD是正方形

∴AB=AD，∠D=∠ABE=90°

∴Rt△AEB≌Rt△AND

∴AE=AN，∠EAB=∠NAD

∴∠EAM=∠NAM=45°

∵AM=AM

∴△AEM≌△ANM

∵AB、AH是△AEM和△ANM对应边上的高，

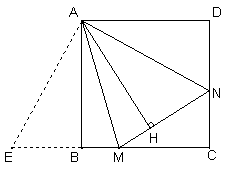∴AB=AH

（3）如图③分别沿AM、AN翻折△AMH和△ANH，

得到△ABM和△AND

∴BM=2，DN=3，∠B=∠D=∠BAD=90°

分别延长BM和DN交于点C，得正方形ABCE．

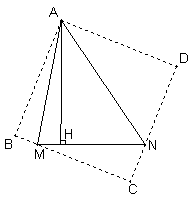由（2）可知，AH=AB=BC=CD=AD.                          

  设AH=x，则MC=,  NC=                             图②

在Rt⊿MCN中，由勾股定理，得

∴

解得.（不符合题意，舍去）

∴AH=6.