
题目列表(包括答案和解析)
 ,
, ,
, 。
。 ,
, ,
, ,x2=-
,x2=- ,x3=
,x3= ,x4=-
,x4=- 。
。.阅读材料,回答问题。
为了解方程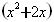
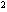 -4
-4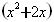 +3=0,我们可以把
+3=0,我们可以把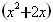 看成一个整体,并设x
看成一个整体,并设x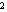 +2x=y,则原方程可化为y
+2x=y,则原方程可化为y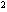 -4y+3=0①,解得y
-4y+3=0①,解得y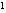 =1,y
=1,y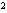 =3
=3
当y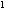 =1时,x
=1时,x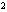 +2x=1,解得x
+2x=1,解得x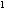 =
=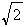 -1,x
-1,x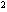 =-
=-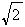 -1;
-1;
当y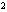 =3时,x
=3时,x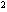 +2x=3,解得x
+2x=3,解得x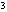 =-3,x
=-3,x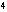 =1。
=1。
故原方程的解为x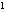 =
=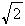 -1,x
-1,x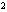 =-
=-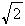 -1,x
-1,x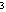 =-3,x
=-3,x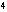 =1
=1 由原方程转化为方程①,这种方法,我们叫做换元法,换元的目的是
由原方程转化为方程①,这种方法,我们叫做换元法,换元的目的是 。
。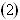 已知
已知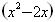
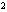 +
+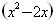 -2=0,求x
-2=0,求x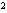 ?2x的值。
?2x的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com