如图，点A是△ABC和△ADE的公共顶点，∠BAC＋∠DAE＝180°，AB＝k?AE，AC＝k?AD，点M是DE的中点，直线AM交直线BC于点N．

⑴探究∠ANB与∠BAE的关系，并加以证明．

说明：如果你经过反复探索没解决问题，可以从下面①②中选取一个作为已知条件，再完成你的证明，选取①比选原题少得2分，选取②比选原题少得5分．

①     如图18，k＝1；②如图19，AB＝AC．

⑵若△ADE绕点A旋转，其他条件不变，则在旋转的过程中⑴的结论是否发生变化？如果没有发生变化，请写出一个可以推广的命题；如果有变化，请画出变化后的一个图形，并直接写出变化后∠ANB与∠BAE的关系．

 

请看下面的问题：把分解因式分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢?19世纪的法国数学家苏菲?热门抓住了该式只有两项，而且属于平方和的形式，要使用公式就必须添一项，随即将此项减去，即可得人们为了纪念苏菲?热门给       出这一解法，就把它叫做“热门定理”，请你依照苏菲?热门的做法，将下列各式因式分解．

(1)                        (2)

阅读材料：如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为P，

求证：S_{四边形ABCD}=AC?BD．

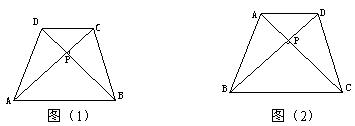
证明：∵AC⊥BD，∴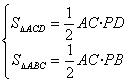

∴S_{四边形ABCD}=S_△ACD+ S_△ABC=AC?PD+AC?PB=AC（PD+PB）=AC?BD。

解答问题：

（1）上述证明得到的性质可叙述为：            ．

（2）已知：如图（2），等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积。

如下图（1），由直角三角形边角关系，可将三角形面积公式变形，

得  =bc?sin∠A．     ①

即三角形的面积等于两边之长与夹角正弦之积的一半．

如下图（2），在ABC中，CD⊥AB于D，∠ACD=α， ∠DCB=β．

∵ ， 由公式①，得

AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ，

即 AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ．   ②

你能利用直角三角形边角关系，消去②中的AC、BC、CD吗？不能，说明理由；能，写出解决过程．