
题目列表(包括答案和解析)
已知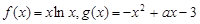
(1)求函数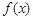 在
在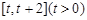 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有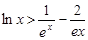 成立
成立
【解析】第一问中利用
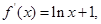 当
当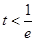 时,
时,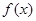 在
在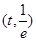 单调递减,在
单调递减,在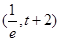 单调递增
单调递增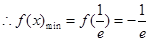 ,当
,当
 ,即
,即 时,
时,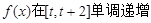 ,
,
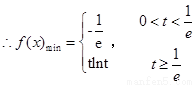
第二问中,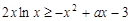 ,则
,则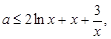 设
设 ,
,
则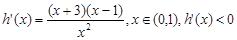 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,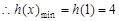 ,因为对一切
,因为对一切 ,
,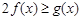 恒成立,
恒成立,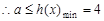
第三问中问题等价于证明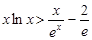 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则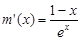 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)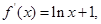 当
当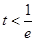 时,
时,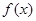 在
在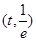 单调递减,在
单调递减,在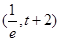 单调递增
单调递增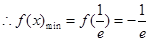 ,当
,当
 ,即
,即 时,
时,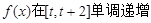 ,
,
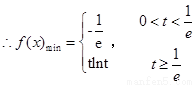 …………4分
…………4分
(2)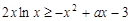 ,则
,则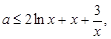 设
设 ,
,
则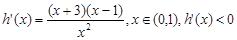 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,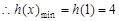 ,因为对一切
,因为对一切 ,
,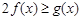 恒成立,
恒成立,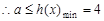 …………9分
…………9分
(3)问题等价于证明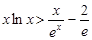 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则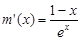 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
(本小题8分)书架上有10本不同的书,其中语文书4本,数学书3本,英语书3本,现从中取出3本书.求:
( 1 )3本书中至少有1本是数学书的概率;
( 2 ) 3本书不全是同科目书的概率.
解:(1)3本书中至少有1本是数学书的概率为
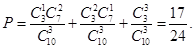 (4分)
(4分)
或解 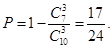 (4分)
(4分)
(2)事件“3本书不全是同科目书”的对立事件是事件“3本书是同科目书”,
而事件“3本书是同科目书”的概率为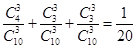 (7分
(7分
∴3本书不全是同科目书的概率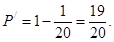 (8分)
(8分)
设函数
(1)当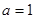 时,求曲线
时,求曲线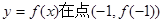 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数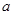 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点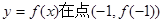 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数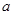 的取值范围是
的取值范围是
如图, ,
,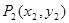 ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,…
均为斜边在
,…
均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

【解析】第一问利用有 ,
, 得到
得到
第二问证明:①当 时,可求得
时,可求得 ,命题成立;②假设当
,命题成立;②假设当 时,命题成立,即有
时,命题成立,即有 则当
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得
第三问

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即

解:(1)依题意,有 ,
, ,………………4分
,………………4分
(2)证明:①当 时,可求得
时,可求得 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当 时,命题成立,即有
时,命题成立,即有 ,……………………1分
,……………………1分
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得 .
.
即
解得 (
( 不合题意,舍去)
不合题意,舍去)
即当 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即
 .……………2分
.……………2分
由题意,有
 .
所以,
.
所以,
已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
【解析】第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中, 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3) 又
又 


 ①
①  ②
②
①- ②得到


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com