
题目列表(包括答案和解析)
 ,
, ,
, 为常数,离心率为
为常数,离心率为 的双曲线
的双曲线 :
: 上的动点
上的动点 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为 ,抛物线
,抛物线 :
:
 的焦点与双曲线
的焦点与双曲线 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线 :
: (
( 为负常数)上任意一点
为负常数)上任意一点 向抛物线
向抛物线 引两条切线,切点分别为
引两条切线,切点分别为 、
、 ,坐标原点
,坐标原点 恒在以
恒在以 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
第二问中, 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得:
借助于根与系数的关系得到即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即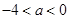
解:(Ⅰ)由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
(Ⅱ)设 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得: ,
,
即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即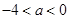
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
如图,在四棱锥P-ABCD中,则面PAD⊥底面 ABCD,
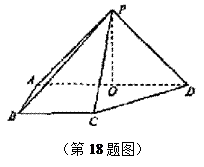
侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中
BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知抛物线C的对称轴与y轴平行,顶点到原点的距离为5,若将抛物线C向上平移3个单位,则在x轴上截得的线段为原抛物线C在x轴上截得的线段的一半;若将抛物线C向左平移1个单位,则所得抛物线过原点,求抛物线C的方程.
|
| α |
|
| β |
|
| π |
| 4 |
| ||
| 2 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com