
题目列表(包括答案和解析)
已知函数 (I)求
(I)求 的单调递增区间;(II)在
的单调递增区间;(II)在 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知,
,已知, 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
已知函数 (I)求
(I)求 的单调递增区间;
的单调递增区间;
(II)在 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知
,已知 ,
, 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
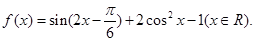 (I)求
(I)求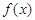 的单调递增区间;
的单调递增区间;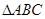 中,三内角
中,三内角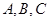 的对边分别为
的对边分别为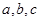 ,已知
,已知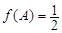 ,
,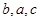 成等差数列,且
成等差数列,且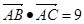 ,求
,求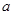 的值
的值 .
.已知函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是[-2,2]。
,单调递减区间是[-2,2]。
(I)求函数![]() 的解析式;
的解析式;
(II)若![]() 的图象与直线
的图象与直线![]() 有三个公共点,求m的取值范围。
有三个公共点,求m的取值范围。
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
一、选择题:本大题共12小题,每小题5分,共60分。
1―5 DCCBD 6―10 ACBBB
二、填空题:本大题共4小题,每小题4分,共16分。
11.1200 12.―3 13.e 14.2 15.16
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分13分)
解:(I)由已知

(II)

|