练习册

  • 练习册
  • 试题
    求出曲线作用下变换得到的曲线方程 (II)选修4―4:坐标系与参数方程 【查看更多】

     

    题目列表(包括答案和解析)

     【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．

    A.选修4-1：几何证明选讲

     

    如图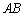，是⊙O的直径，弦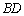、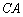的延长线相交于点E，EF垂直BA的延长线于点F．求证：

    （1）；

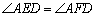    （2）．

     

     

     

     

     

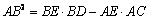    B.选修4-2：矩阵与变换

     

    求曲线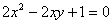在矩阵MN对应的变换作用下得到的曲线方程，其中，．

     

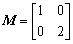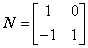    C.选修4-4：坐标系与参数方程

     

    以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的单位长度.已知直线l的极坐标方程为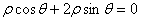，曲线C的参数方程为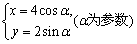，又直线l与曲线C交于A，B两点，求线段AB的长.

     

    D.选修4-5：不等式选讲

     

    若存在实数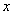使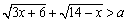成立，求常数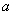的取值范围．

     

     

    查看答案和解析>>

    精英家教网本题有（1），（2），（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑．
    （1）选修4-2：矩阵与变换
    如图所示：△OAB在伸缩变换M作用下变为△OA1B1．
    （i）求矩阵M的特征值及相应的特征向量；
    （ii）求逆矩阵M-1以及（M-1）20
    （2）选修4-4：坐标系与参数方程．
    已知曲线C1的参数方程为
    x=2sinθ
    y=cosθ
    （θ为参数），曲线C2的参数方程为
    x=2t
    y=t+1
    （t为参数）
    （i）若将曲线C1与C2上各点的横坐标都缩短为原来的一半，分别得到曲线C1和C2，求出曲线C1和C2的普通方程；
    （ii）以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，求过极点且与C2垂直的直线的极坐标方程．
    （3）选修4-5：不等式选讲
    已知a，b，c为实数，且a+b+c+2-2m=0，a2+
    b 2
    4
    +
    c 2
    9
    +m-1=0
    （i）求证：a2+
    b 2
    4
    +
    c 2
    9
    ≥
    (a+b+c) 2
    14

    （ii）求实数m的取值范围．

    查看答案和解析>>

    【选做题】在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．
    A．选修4-1　几何证明选讲
    如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
    B．选修4-2　矩阵与变换
    若点A（2，2）在矩阵M=
    cosα-sinα
    sinαcosα
    对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵．
    C．选修4-4　坐标系与参数方程
    已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，
    曲线C1：ρcos(θ+
    π
    4
    )=2
    		2
    与曲线C2：
    x=4t2
    y=4t
    （t∈R）交于A、B两点．求证：OA⊥OB．
    D．选修4-5　不等式选讲
    已知x，y，z均为正数．求证：
    x
    yz
    +
    y
    zx
    +
    z
    xy
    ≥
    1
    x
    +
    1
    y
    +
    1
    z
    ．

    查看答案和解析>>

     

    一、选择题：本大题共12小题，每小题5分，共60分。

    1―5 DCCBD    6―10 ACBBB

    二、填空题：本大题共4小题，每小题4分，共16分。

    11．1200    12．―3    13．e    14．2    15．16

    三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。

    16．（本小题满分13分）

    解：（I）由已知

       （II）

     

       （I）证明：（1）连接CD1

    ∵四棱柱ABCD―A1B1C1D1中，底面ABCD是菱形

    ∴A1D1//AD，AD//BC，A1D1=AD，AD=BC；

    ∴A1D1//BC，A1D1=BC，

    ∴四边形A1BCD1为平行四边形；∴A1B//D1C………3分

    ∵点E、F分别是棱CC1、C1D1的中点；∴EF//D1C

    又∴EF//A1B

    又∵A1B平面A1DB，EF面A1DB；

    ∴EF⊥平面A1BD  ………………6分

       （II）连结AC交BD于点G，连接A1G，EG

    ∵四棱柱ABCD―A1B1C1D1中，A1A⊥底面ABCD，

    底面ABCD是菱形

    ∴AA1⊥AB，AA1⊥AD，EC⊥BC，EC⊥DC，

    AD=AB，BC=CD

    ∵底面ABCD是菱形，∴点G为BD中点，

    ∴A1G⊥BD，EG⊥BD

    ∴∠A1GE为直二面角A1―BD―E的平面角，

    ∴∠A1GE=90°………………3分

    在棱形ABCD中，∠DAB=60°，AB=2，

    ∴∠ABC=120°，

    ∴AC=

    ∴AG=GC=  ………………10分

    在面ACC1A1中，△AGA1，△GCE为直角三角形

    ∵∠A1GE=90°∴∠EGC+∠A1GA=90°，∴∠EGC=∠AA1G，

    ∴Rt△A1AG∽Rt△ECG ………………12分

    解法二：

       （I）证明：取AB的中点G，连接GD

    ∵底面ABCD是菱形，∠DAB=60°，AB=2

    ∴△ABD是正三角形，∴DG⊥AB，DG=

    又∵AB//CD，∴DG⊥DC   …………2分

    ∵四棱柱ABCD―A1B1C1D1为直四棱柱，AA1//DD1

    A1A⊥底面ABCD，∴DD1⊥底面ABCD

    以D为坐标原点，射线DG为x轴的正半轴，射线DC为y轴的正半轴，

    建立如图所示空间直角坐标系D―xyz.

    18．解：（I）掷一枚硬币三次，列出所有可能情况共8种：

       （上上上），（上上下），（上下上），（上下下），（下上上），（下上下），（下下上），（下下下）；

        其中甲得2分、乙得1分的有3种，故所求概率  …………3分

       （II）在题设条件下，至多还要2局，情形一：在第四局，硬币正面朝上，则甲积3分、乙积1分，甲获胜，概率为1/2；情形二：在第四局，硬币正面朝下，第五局硬币正面朝上，则甲积3分、乙积2分，甲获胜，概率为1/4。由加法公式，甲获胜的概率为1/2+1/4=3/4。   ………………8分

       （III）据题意，ξ的取值为3、4、5，

        且   ………………11分

       

        其分布列如下：

    ξ

    3

    4

    5

    P

    1/4

    3/8

    3/8

           ………………13分

    19．解：（I）∵F1，F2三等份BD， …………1分

           ………………3分

       （II）由（I）知为BF2的中点，

       

       （III）依题意直线AC的斜率存在，

     

        同理可求

       

       （III）法二：

       

    20．（I）解：

       （II）切线l与曲线有且只有一个公共点等价

    ①

    的唯一解；  ………………7分

    ②

     

     

    x

    （―1，0）

    0

    +

    0

    ―

    0

    +

    极大值0

    极小值

    ③

    x

    0

    +

    0

    ―

    0

    +

    极大值

    极小值0

       （III）

    21．（I）由已知BA=  ………………2分

    任取曲线

    则有=，即有  ………………5分

      ………………6分

    即   …………①   与   ………………②

    比较①②得

       （II）设圆C上的任意一点的极坐标，过OC的直径的另一端点为B，

    边PO，PB则在直角三角形OPB中， …………5分

    （写不扣分）

    从而有   ………………7分

       （III）证：为定值，

    利用柯西不等式得到

    ………5分

     


    同步练习册答案