
题目列表(包括答案和解析)
a1bn+a2bn-1+a3bn-2+…+an-1b2+anb1=2n+1-n-2.
(1)若数列{an}是首项和公差都是1的等差数列,求证:数列{bn}是等比数列;
(2)若数列{bn}是等比数列,数列{an}是否是等差数列,若是,请求出通项公式;若不是,请说明理由;
(3)若数列{an}是等差数列,数列{bn}是等比数列,求证:![]() <
<![]() .
.
| -2x+3 |
| 2x-7 |
| 1 |
| 2 |
| 7 |
| 2 |
| f(x)-a |
| f(x)-b |
| 8(x-a) |
| x-b |
| 1 |
| 2 |
| 7 |
| 2 |
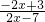 ,若存在实数x0,使f(x0)=x0则称x0是函数y=f(x)的一个不动点.
,若存在实数x0,使f(x0)=x0则称x0是函数y=f(x)的一个不动点. ≠
≠ 时,比较
时,比较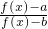 与
与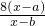 的大小;
的大小; 且an≠
且an≠ ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.已知函数f(x)=![]() ,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点.
,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点.
(Ⅰ)证明:函数y=f(x)有两个不动点;
(Ⅱ)已知a、b是y=f(x)的两个不动点,且a>b.当x≠-![]() 且x≠
且x≠![]() 时,比较
时,比较![]() 与
与![]() 的大小;
的大小;
(Ⅲ)在数列{an}中,an≠-![]() 且an≠
且an≠![]() ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式.
| n |
 |
| i=1 |
| 1 |
| aibi |
| 3 |
| 2 |
1.3; 2 . -1; 3. -2;4.数学.files/image117.gif) 5.3 6.
5.3 6.数学.files/image119.gif) 7 .
7 .数学.files/image121.gif)
8. 数学.files/image123.gif) 9. (0,1) 10.
9. (0,1) 10. 数学.files/image125.gif) 11.
11.
数学.files/image127.gif) .
.
12. 数学.files/image129.gif) ;13.
;13. 数学.files/image131.gif) ;14.
;14. 数学.files/image133.gif) ;
;
15.解:(Ⅰ)由题意知数学.files/image135.gif)
数学.files/image137.gif)
数学.files/image139.gif)
……………………3分
数学.files/image141.gif)
数学.files/image143.gif) ……………………4分
……………………4分
数学.files/image145.gif) 的夹角
的夹角
数学.files/image147.gif)
数学.files/image149.gif) ……………………7分
……………………7分
(Ⅱ)数学.files/image151.gif)
数学.files/image153.gif) ……………………10分
……………………10分
数学.files/image155.gif)
数学.files/image157.gif)
数学.files/image159.gif) 有最小值。
有最小值。
数学.files/image161.gif) 的最小值是
的最小值是数学.files/image163.gif) ……………………14分
……………………14分
16.解:(1)【证明】因为∠ABC=90°,AD∥BC,所以AD⊥AB.
而平面PAB⊥平面ABCD,且平面PAB数学.files/image079.gif) 平面ABCD=AB,
平面ABCD=AB,
所以AD⊥平面PAB, 所以AD⊥PA. ………………3分
同理可得AB⊥PA. ………………5分
由于AB、AD数学.files/image165.gif) 平面ABCD,且AB
平面ABCD,且AB数学.files/image079.gif) AD=C,
AD=C,
所以PA⊥平面ABCD. ………………………7分
(2)【解】(方法一)不平行. ………………………9分
证明:假定直线l∥平面ABCD,
由于l数学.files/image165.gif) 平面PCD,且平面PCD
平面PCD,且平面PCD数学.files/image079.gif) 平面ABCD=CD, 所以
平面ABCD=CD, 所以数学.files/image167.gif) ∥CD. ……………… 11分
∥CD. ……………… 11分
同理可得l∥AB, 所以AB∥CD. …………………… 13分
这与AB和CD是直角梯形ABCD的两腰相矛盾,
故假设错误,所以直线l与平面ABCD不平行. …………………… 14分
(方法二)因为梯形ABCD中AD∥BC,
所以直线AB与直线CD相交,设AB数学.files/image079.gif) CD=T.
…………………… 11分
CD=T.
…………………… 11分
由T数学.files/image170.gif) CD,CD
CD,CD数学.files/image165.gif) 平面PCD得T
平面PCD得T数学.files/image170.gif) 平面PCD.
平面PCD.
同理T数学.files/image170.gif) 平面PAB.
…………………… 13分
平面PAB.
…………………… 13分
即T为平面PCD与平面PAB的公共点,于是PT为平面PCD与平面PAB的交线.
所以直线数学.files/image167.gif) 与平面ABCD不平行.
…………………… 14分
与平面ABCD不平行.
…………………… 14分
17.解:(1)依题意数列数学.files/image083.gif) 的通项公式是
的通项公式是数学.files/image173.gif) ,
,
故等式即为数学.files/image175.gif) ,
,
同时有数学.files/image177.gif)
数学.files/image179.gif) ,
,
两式相减可得数学.files/image181.gif) ………………………………3分
………………………………3分
可得数列数学.files/image085.gif) 的通项公式是
的通项公式是数学.files/image183.gif) ,
,
知数列数学.files/image085.gif) 是首项为1,公比为2的等比数列。 ………………………6分
是首项为1,公比为2的等比数列。 ………………………6分
(2)设等比数列数学.files/image085.gif) 的首项为
的首项为数学.files/image185.gif) ,公比为
,公比为数学.files/image187.gif) ,则
,则数学.files/image189.gif) ,从而有:
,从而有:
数学.files/image191.gif) ,
,
又数学.files/image193.gif)
数学.files/image179.gif) ,
,
故数学.files/image195.gif) ……………………………9分
……………………………9分
数学.files/image197.gif) ,
,
要使数学.files/image199.gif) 是与
是与数学.files/image067.gif) 无关的常数,必需
无关的常数,必需数学.files/image202.gif) , …………………………11分
, …………………………11分
即①当等比数列数学.files/image085.gif) 的公比
的公比数学.files/image202.gif) 时,数列
时,数列数学.files/image083.gif) 是等差数列,其通项公式是
是等差数列,其通项公式是数学.files/image206.gif) ;
;
②当等比数列数学.files/image085.gif) 的公比不是2时,数列
的公比不是2时,数列数学.files/image083.gif) 不是等差数列. ………………14分
不是等差数列. ………………14分
18.解:(Ⅰ)当9天购买一次时,该厂用于配料的保管费用
P=70+数学.files/image208.gif) =88(元)
……………………………4分
=88(元)
……………………………4分
(Ⅱ)(1)当x≤7时
y=360x+10x+236=370x+236 ………………5分
(2)当 x>7时
y=360x+236+70+6[(数学.files/image210.gif) )+(
)+(数学.files/image212.gif) )+……+2+1]
)+……+2+1]
=数学.files/image214.gif) ………………7分
………………7分
∴数学.files/image216.gif) ………………8分
………………8分
∴设该厂x天购买一次配料平均每天支付的费用为f(x)元
数学.files/image218.gif) ………………11分
………………11分
当x≤7时
数学.files/image220.gif) 当且仅当x=7时
当且仅当x=7时
f(x)有最小值数学.files/image222.gif) (元)
(元)
当x>7时
数学.files/image224.gif) =
=数学.files/image226.gif) ≥393
≥393
当且仅当x=12时取等号
∵393<404
∴当x=12时 f(x)有最小值393元 ………………16分
19.解:(1)设椭圆数学.files/image096.gif) 的焦距为
的焦距为
则其右准线方程为x=数学.files/image228.gif) ,且F1(-c, 0), F2(c, 0).
……………2分
,且F1(-c, 0), F2(c, 0).
……………2分
设M数学.files/image230.gif) ,
,
则数学.files/image232.gif) =
=数学.files/image234.gif)
数学.files/image236.gif) .
……………………4分
.
……………………4分
因为数学.files/image099.gif) ,所以
,所以数学.files/image238.gif) ,即
,即数学.files/image240.gif) .
.
于是数学.files/image242.gif) ,故∠MON为锐角.
,故∠MON为锐角.
所以原点O在圆C外. ………………………7分
(2)因为椭圆的离心率为数学.files/image101.gif) ,所以a=
,所以a=
于是M 数学.files/image244.gif) ,且
,且数学.files/image246.gif) ………………………9分
………………………9分
MN2=(y1-y2)2=y12+y22-2y1y2数学.files/image248.gif) .………… 12分
.………… 12分
当且仅当
y1=-y2=数学.files/image250.gif) 或y2=-y1=
或y2=-y1=数学.files/image250.gif) 时取“=”号,
………………… 14分
时取“=”号,
………………… 14分
所以(MN)min=
故所求的椭圆方程是数学.files/image252.gif) . ………………… 16分
. ………………… 16分
22.解:(Ⅰ)数学.files/image254.gif) ,………………………………1分
,………………………………1分
又数学.files/image256.gif) ,
,
数学.files/image258.gif) 处的切线方程为
处的切线方程为
数学.files/image260.gif) ………………………3分
………………………3分
(Ⅱ)数学.files/image262.gif) ,
,
数学.files/image264.gif) …………………………………………4分
…………………………………………4分
令数学.files/image266.gif) ,
,
则数学.files/image268.gif) 上单调递增,
上单调递增,
数学.files/image270.gif) 上存在唯一零点,
上存在唯一零点,数学.files/image272.gif) 上存在唯一的极值点………6分
上存在唯一的极值点………6分
取区间数学.files/image274.gif) 作为起始区间,用二分法逐次计算如下
作为起始区间,用二分法逐次计算如下
区间中点坐标
中点对应导数值
取区间数学.files/image276.gif)
数学.files/image278.gif)
数学.files/image274.gif)
1
数学.files/image281.gif)
数学.files/image283.gif)
数学.files/image285.gif)
0.6
数学.files/image287.gif)
数学.files/image289.gif)
数学.files/image291.gif)
0.3
数学.files/image293.gif)
由上表可知区间数学.files/image291.gif) 的长度为0.3,所以该区间的中点
的长度为0.3,所以该区间的中点数学.files/image296.gif) ,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。
,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个极值点的相应x的值。
数学.files/image298.gif) 取得极值时,相应
取得极值时,相应数学.files/image300.gif) ………………………9分
………………………9分
(Ⅲ)由数学.files/image302.gif) ,
,
即数学.files/image304.gif) ,
,
数学.files/image306.gif) ,………………………………………12分
,………………………………………12分
令数学.files/image308.gif)
令数学.files/image310.gif)
数学.files/image312.gif) 上单调递增,
上单调递增,
数学.files/image314.gif) ,
,
因此数学.files/image316.gif) 上单调递增,
上单调递增,
则数学.files/image318.gif) ,
,
数学.files/image320.gif) 的取值范围是
的取值范围是
数学.files/image322.gif) ………………………………………16分
………………………………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com