
题目列表(包括答案和解析)
给定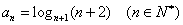 ,定义使乘积
,定义使乘积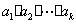 为整数的
为整数的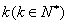 叫做希望数,则区间
叫做希望数,则区间 内的所有希望数的和为( )
内的所有希望数的和为( )
A.2005 B.2026 C.2016 D.2006
已知数列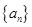 的通项为
的通项为 ,我们把使乘积
,我们把使乘积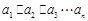 为整数的
为整数的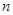 叫做“优数”,则在
叫做“优数”,则在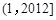 内的所有“优数”的和为( )
内的所有“优数”的和为( )
A.1024 B.2012 C.2026 D.2036
给定![]()
![]() ,定义乘积
,定义乘积![]() 为整数的
为整数的![]() 叫做希望数,则区间
叫做希望数,则区间![]() 内的所有希望数之和为________.
内的所有希望数之和为________.
已知数列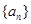 满足:
满足: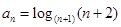 ,定义使
,定义使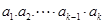 为整数的
为整数的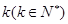 叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
叫做希望数,则区间[1,2013] 内所有希望数的和M=( )
A.2026 B.2036 C.32046 D.2048
已知数列 满足
满足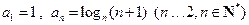 .定义:使
.定义:使
乘积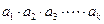 为正整数的
为正整数的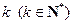 叫做“和谐数”,则在区间
叫做“和谐数”,则在区间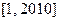 内所有的“和谐数”的和为
内所有的“和谐数”的和为
A.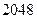 | B.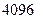 | C.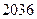 | D.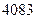 |
一、 选择题(每小题5分,共60分)
CADACD CDBDBA
二、填空题(每小题4分,共16分)
13. 14.
14. 15.
15. 16.
16.
三、解答题
17.(本小题满分12分)
解:(Ⅰ)∵ ,
,
由 ,得
,得
两边平方: =
= ,∴
,∴ =
= ………………6分
………………6分
(Ⅱ)∵ ,
,
∴ ,解得
,解得 ,
,
又∵ ,
∴
,
∴ ,
,
∴ ,
, ,
,
设 的夹角为
的夹角为 ,则
,则
 ,∴
,∴
即 的夹角为
的夹角为 . …………… 12分
. …………… 12分
18. (本小题满分12分)
解:(Ⅰ)小王在一年内领到驾照的概率为:
 ………………………(
4分)
………………………(
4分)
(Ⅱ) 的取值分别为1,2,3.
的取值分别为1,2,3.
 ,
,
 ………………………(
8分)
………………………(
8分)
所以小王参加考试次数 的分布列为:
的分布列为:

1
2
3

0.6
0.28
0.12
所以 的数学期望为
的数学期望为 ……………………12分
……………………12分
19.(本小题满分12分)
(Ⅰ)证明:由已知得 ,所以
,所以 ,即
,即 ,
,
又 ,
, ,∴
,∴ ,
,
 平面
平面
∴平面 平面
平面 .……………………………4分(文6分)
.……………………………4分(文6分)
(Ⅱ)解:设 的中点为
的中点为 ,连接
,连接 ,则
,则 ∥
∥ ,
,
∴ 是异面直线
是异面直线 和
和 所成的角或其补角
所成的角或其补角
由(Ⅰ)知 ,在
,在 中,
中, ,
, ,
,
∴ .
.
所以异面直线 和
和 所成的角为
所成的角为 .…………………8分(文12分)
.…………………8分(文12分)
(Ⅲ)(解法一)由已知得四边形 是正方形,
是正方形,
∴ 又
又 ,∴
,∴ ,
,
过点 做
做 于
于 ,连接
,连接 ,则
,则 ,
,
则 即二面角
即二面角 的平面角,
的平面角,
在 中,
中, ,所以
,所以 ,
,
又 ,由余弦定理得
,由余弦定理得 ,
,
所以二面角 的大小为
的大小为 .……………12分
.……………12分
(解法二)向量法
设 为
为 的中点,则
的中点,则 ,以
,以 为坐标原点,
为坐标原点, 所在直线分别为
所在直线分别为 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则
 ,
,

设平面 的法向量
的法向量
由 得
得 由
由 得
得 所以
所以
同理得平面 的法向量
的法向量
 ,
,
所以所求二面角的大小为 .………………12分
.………………12分
20.(本小题满分12分)
解:(Ⅰ)
当 时,
时, ,∴
,∴ .
.
当

 ……………6分
……………6分
(Ⅱ)当 时,由(Ⅰ)的讨论可知
时,由(Ⅰ)的讨论可知
即
∴




∴ ………………12分
………………12分
21.(本小题满分12分)
解:(Ⅰ)∵
∴
∴
令 ,则
,则 ,∴
,∴
 ,∴
,∴
∴ .……………6分
.……………6分
(Ⅱ)证明:


∴
又∵ ,∴
,∴
∴
∴ .………………12分
.………………12分
22.(本小题满分14分)
解:(Ⅰ)①当直线 轴时,
轴时,
则 ,此时
,此时 ,∴
,∴ .
.
(不讨论扣1分)
②当直线 不垂直于
不垂直于 轴时,
轴时, ,设双曲线的右准线为
,设双曲线的右准线为 ,
,
作 于
于 ,作
,作 于
于 ,作
,作 于
于 且交
且交 轴于
轴于
根据双曲线第二定义有: ,
,
而 到准线
到准线 的距离为
的距离为 .
.
由 ,得:
,得: ,
,
∴ ,∴
,∴ ,∵此时
,∵此时 ,∴
,∴
综上可知 .………………………………………7分
.………………………………………7分
(Ⅱ)设 :
: ,代入双曲线方程得
,代入双曲线方程得
∴
令 ,则
,则 ,且
,且 代入上面两式得:
代入上面两式得:
 ①
①
 ②
②
由①②消去 得
得
即 ③
③
由 有:
有: ,综合③式得
,综合③式得
由 得
得 ,解得
,解得
∴ 的取值范围为
的取值范围为 …………………………14分
…………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com