若点P是以F₁，F₂为焦点的椭圆＋＝1(a＞b＞0)上一点，且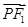·＝0，tan∠PF₁F₂＝则此椭圆的离心率e＝（    ）

A、            B、          C、          D、

在正三棱锥P－ABC中，PA＝，，点E、F分别在侧棱PB、PC上，则周长的最小值为　　　　.

已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)＝－，其中e是自然常数，a∈R．

（1）讨论a＝－1时, f (x)的单调性、极值；

（2）求证：在（1）的条件下，|f (x)|＞g(x)＋1/2；

（3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．

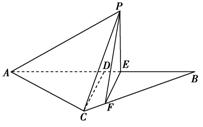
如右图所示，等腰三角形△ABC的底边AB＝6，高CD＝3，

点E是线段BD上异于B、D的动点，点F在BC边上，且EF⊥AB，现沿EF将△BEF折起到△PEF的位置，使PE⊥AE，记BE＝x，V(x)表示四棱锥P－ACEF的体积．

 (1)求V(x)的表达式；

 (2)当x为何值时，V(x)取得最大值？

 (3)当V(x)取得最大值时，求异面直线AC与PF所成角的余弦值

已知tanα＝4，cotβ＝，则tan（α＋β）等于         （      ）

    A、          B、－          C、          D、－