题目列表(包括答案和解析)
如图所示，每米电阻为lΩ的一段导线被弯成半径r=lm的三段圆弧组成闭合回路．每段圆弧都是| 1 |
| 4 |
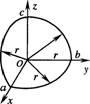如图所示，每米电阻为lΩ的一段导线被弯成半径r=1m的三段圆弧组成闭合回路．每段圆弧都是1/4圆周，位于空间直角坐标系的不同平面内：ab段位于xoy平面内，bc段位于yoz平面内，ca段位于zox平面内．空间内存在着一个沿x轴正方向的匀强磁场，其磁感应强度B随时间t变化的关系式为Bt=0.7+0.6t(T)．则
A．导线中的感应电流大小是0.1A，方向是a→c→b→a
B．导线中的感应电流大小是0.1A，方向是a→b→c→a
C．导线中的感应电流大小是（π/20）A，方向是a→c→b→a
D．导线中的感应电流大小是（π/20）A，方向是a→b→c→a
如图8所示，每米电阻为lΩ的一段导线被弯成半径r=lm的三段圆弧组成闭合回路．每段圆弧都是
圆周，位于空间直角坐标系的不同平面内：ab曲段位于．xoy平面内，bc段位于yoz平面内，ca段位于zox平面内．空间内存在着一个沿+x轴方向的磁场，其磁感应强度随时间变化的关系式为Bt=0.7+0.6t(T)。则 （ ）
A．导线中的感应电流大小是0.1A，方向是a→c→b→a
B．导线中的感应电流大小是0.1A，方向是a→b→c→a
C．导线中的感应电流大小是
A，方向是a→c→b→a
D．导线中的感应电流大小是A，方向是a→b→c→a
圆周，位于空间直角坐标系的不同平面内：ab曲段位于．xoy平面内，bc段位于yoz平面内，ca段位于zox平面内．空间内存在着一个沿+x轴方向的磁场，其磁感应强度随时间变化的关系式为Bt=0.7+0.6t(T)。则（）
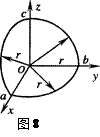
| A．导线中的感应电流大小是0.1A，方向是a→c→b→a |
| B．导线中的感应电流大小是0.1A，方向是a→b→c→a |
C．导线中的感应电流大小是 A，方向是a→c→b→a |
| D．导线中的感应电流大小是A，方向是a→b→c→a |
(12分)在探究“决定导体电阻的因素”实验中，我们经常用到刻度尺、游标卡尺、螺旋测微器、电压表、电流表等测量工具。
(1)在一次实验中，如果提供了下列几个长度测量仪器：①毫米刻度尺；②10分度游标卡尺；③20分度游标卡尺；④螺旋测微器。一个同学用其中一种仪器正确测量某工件的长度为3.125 cm，则他所使用的仪器为 (填仪器序号)。如图是用螺旋测微器测量的电阻丝直径的示意图，则该电阻丝的直径
= mm。
(2)某研究性学习小组的同学想测量某电阻丝的电阻率。
①同学们截取了约1m长的电阻丝，首先利用多用电表的欧姆挡粗测其阻值，下列操作或说法中正确的是
A．测量前检查表针是否停在左端的“0”位置，如不在则要进行欧姆调零
B．若用欧姆表“×l”挡测量，指针恰好在刻度30～50的正中，则待测电阻为40Ω
C．若用欧姆表“×10”挡测量，指针偏转角度过大，应换成“×1”挡
D．每次改变不同倍率的欧姆档后都要重新进行欧姆调零
②若同学们粗测得该段电阻丝的阻值约为3Ω，然后用伏安法测定电阻丝的阻值，再利用公式
求得电阻丝的电阻率
。可供选择的器材如下：
A．量程0．6A，内阻0.5Ω的电流表
B．量程3 A，内阻0.1Ω的电流表
C．量程3 V，内阻6 kΩ的电压表
D．量程15V，内阻30kΩ的电压表
E．阻值为0～1 kΩ，额定电流为0.5A的滑动变阻器
F．阻值为0～10Ω，额定电流为1 A的滑动变阻器
G．6 V蓄电池
H．电键一个、导线若干
实验中要求金属丝的发热功率不超过0.75 W，电流表应选用 ；电压表应选用 ；滑动变阻器应选用 。(请填写备选器材前的字母)
一、全题共计15分,每小题3分: 1.D 2.B 3.A 4.C 5.D
二、全题共计16分,每小题4分，漏选的得２分: 6.AD 7.BD 8. ABD 9.BD
三、全题共计42分
10.（8分）⑴20.30 ⑵①S1/2T；② 9.71～9.73 ③阻力作用 (每空2分)
11．（10分）第⑶问4分，其中作图2分；其余每小问2分．⑶半导体材料 ⑷4.0 、 0.40
12．(12分) ⑴D （3分） ⑵AC（3分）
⑶这种解法不对．
错在没有考虑重力加速度与高度有关(2分)
正确解答：卫星绕地球做匀速圆周运动，万有引力提供向心力，根据牛顿第二定律有
G
=mA
③
G
=mB
④ 由③④式，得 
（4分）
13A.(12分) ⑴不变（2分） 50（2分） ⑵a→b（2分） 增加（2分） ⑶
（4分）
13B.(12分) ⑴C（3分 ） ⑵60°（2分） 偏右（2分） ⑶
（2分） 0.25s（3分）
13C.(12分) ⑴质子 、α 、氮 ⑵ mv2/4 ⑶a 、 5×1013 （每空2分）
四、全题共计47分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位
14.(15分) 解：⑴A→C过程，由动能定理得：
………… （3分）
△R= R (1－cos37°)……………… （1分） ∴ vc=14m/s …………………… （1分）
⑵在C点，由牛顿第二定律有： 
……（2分）
∴ Fc=3936N …………………………………………………………………………（ 2分）
由牛顿第三定律知，运动员在C点时轨道受到的压力大小为3936N. …………… （1分）
⑶设在空中飞行时间为t，则有：tan37°=
………………… （ 3分）
∴t = 2.5s (t =－0.4s舍去)……………………………………………………（ 2分）
15.(16分) 解：⑴垂直AB边进入磁场，由几何知识得：粒子离开电场时偏转角为30°
∵
………（2分）
……… （1分） ∴
………（2分）
由几何关系得：
在磁场中运动半径
……（2分）
∴ 
……………………………（2分）
∴
……………（1分 ） 方向垂直纸面向里……………………（1分）
⑶当粒子刚好与BC边相切时，磁感应强度最小，由几何知识知粒子的运动半径r2为：
………（ 2分 ） 
………1分 ∴
……… 1分
即：磁感应强度的最小值为
………（1分）
16．(16分)
解：⑴据能量守恒，得 △E
= mv02
-
m（）2= mv02-----------（3分）
⑵在底端，设棒上电流为I，加速度为a，由牛顿第二定律，则：
（mgsinθ+BIL）=ma1--------------------------（1分）
由欧姆定律，得I=---------------（1分） E=BLv0---------------------（1分）
由上述三式，得a1 = gsinθ + ---------------------（1分）
∵棒到达底端前已经做匀速运动∴mgsinθ= ------------------------------（1分）
代入，得a1 = 5gsinθ-----------------------------------------（2分）
（3）选沿斜面向上为正方向，上升过程中的加速度，上升到最高点的路程为S，
a = －（gsinθ + ）-----------------------（1分）
取一极短时间△t，速度微小变化为△v，由△v = a△t，得
△ v = －（ gsinθ△t+B2L2v△t/mR）-----------（1分）
其中，v△t = △s--------------------------（1分）
在上升的全过程中
∑△v = －（gsinθ∑△t+B2L2∑△s/mR）
即 0-v0= －（t0gsinθ+B2L2S/mR）-------------（1分）
∵H=S?sinθ 且gsinθ= -------------------（1分）
∴ H =（v02-gv0t0sinθ）/4g-----------------（1分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com