
题目列表(包括答案和解析)
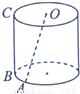
 (2013•上海)已知圆柱Ω的母线长为l,底面半径为r,O是上底面圆心,A,B是下底面圆周上两个不同的点,BC是母线,如图,若直线OA与BC所成角的大小为
(2013•上海)已知圆柱Ω的母线长为l,底面半径为r,O是上底面圆心,A,B是下底面圆周上两个不同的点,BC是母线,如图,若直线OA与BC所成角的大小为| π |
| 6 |
| l |
| r |
| 3 |
| 3 |
如图,已知圆![]() 与
与![]() 轴负半轴的交点为
轴负半轴的交点为![]() . 由点
. 由点![]() 出发的射线
出发的射线![]() 的斜率为
的斜率为![]() . 射线
. 射线![]() 与圆
与圆![]() 相交于另一点
相交于另一点![]()

(1)当![]() 时,试用
时,试用![]() 表示点
表示点![]() 的坐标;
的坐标;
(2)当![]() 时,求证:“射线
时,求证:“射线![]() 的斜率
的斜率![]() 为有理数”是“点
为有理数”是“点![]() 为单位圆
为单位圆![]() 上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为
上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为![]() ,其中
,其中![]() 、
、![]() 均为整数且
均为整数且![]() 、
、![]() 互质)
互质)
(3)定义:实半轴长![]() 、虚半轴长
、虚半轴长![]() 和半焦距
和半焦距![]() 都是正整数的双曲线为“整勾股双曲线”.
都是正整数的双曲线为“整勾股双曲线”.
当![]() 为有理数且
为有理数且![]() 时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点
时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点![]() 的横坐标、纵坐标和半径
的横坐标、纵坐标和半径![]() 的数值构成. 说明你的理由并请尝试给出构造方法.
的数值构成. 说明你的理由并请尝试给出构造方法.
已知圆柱Ω的母线长为l,底面半径为r,O是上底面圆心,A,B是下底面圆周上两个不同的点,BC是母线,如图,若直线OA与BC所成角的大小为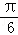 ,则
,则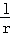 = .
= .
已知二次函数 的图象如图所示,则它与
的图象如图所示,则它与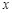 轴所围图形的面积为:
轴所围图形的面积为:
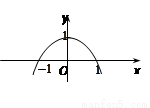
A.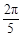 B.
B.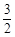 C.
C.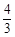 D.
D.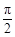
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com