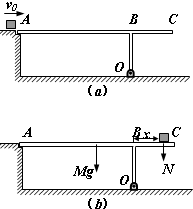如图（a）所示，ABCO是固定在一起的T型支架，其中水平部分AC是质量为M=2kg、长度为L=1m的匀质薄板，OB是轻质硬杆，下端通过光滑铰链连接在水平地面上，可绕水平轴O在竖直面内自由转动，支架A端搁在左侧平台上．已知AB的长度l₁=

3

4

L，OB的长度h=0.5m．现有一质量为m=2kg的钢块（可看成质点）以v₀=3m/s的水平初速度滑上AC板，钢块与板间动摩擦因数μ=0.5．问：T型支架会不会绕O轴翻转？（g=10m/s²）
某同学的解题思路如下：
支架受力情况如图（b），设支架即将翻转时钢块位于B右侧x处，根据力矩平衡的方程：
M_g（l₁-

L

2

）=N?x，式中N=mg，
解得x=0.2m．
此时钢块离A端
s₁=

3

4

L+x=0.95m．
然后算出钢块以v₀=3m/s的初速度在AC板上最多能滑行的距离s₂；
…
比较这两个距离：
若s₂≤s₁，则T型支架不会绕O轴翻转；
若s₂＞s₁，则会绕O轴翻转．
请判断该同学的解题思路是否正确．若正确，请按照该思路，将解题过程补充完整，并求出最后结果；若不正确，请用自己的方法算出正确的结果．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

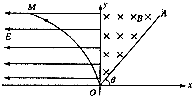如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky²（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
（1）求带电粒子穿越y轴时的速度与释放点纵坐标的关系式；
（2）若粒子从OM上任何位置释放，要求粒子穿过磁场区域后，都垂直于x轴射出求直线OA与x轴的夹角正切值tanθ（用题中已知物理量的符号表示）

查看答案和解析>>

如图所示，质量M=4kg的木板AB静止放在光滑水平上，木板右端B点固定着一根轻质弹簧，弹簧自由端在C点，C到木板左端的距离L=0.5m，质量m=1kg的小木块（可视为质点）静止在木板的左端，其与木板间的动摩擦因数μ=0.2．木板AB受到水平向左的恒力F=14N，作用时间t后撤去，恒力F撤去时小木块恰好到达弹簧的自由端C处，此后的运动过程中弹簧的最大压缩量x=5cm，取g=10m/s²．试求：
（1）水平恒力F作用的时间
（2）弹簧的最大弹性势能
（3）通过计算确定小木块最终停在C点的左边还是右边，并求出整个运动过程中所产生的热量．

查看答案和解析>>

1．B　２．Ａ　3．B   4． B   5．C   6．B   7．D  8．ABD ．ABC   10．D

11．  丙   错误操作是先放开纸带后接通电源。

(1)左；(2)

(3)    

(4) ΔE_P>ΔE_K这是因为实验中有阻力。

(5)在实验误差允许围内，机械能守恒

12．（１）用天平分别测出滑块Ａ、Ｂ的质量、

　　　（２）

　　　（３）

由能量守恒知

13．解：（１）设小球摆回到最低点的速度为ｖ，绳的拉力为Ｔ，从Ｆ开始作用到小球返回到最低点的过程中，运用动能定理有，在最低点根据牛顿第二定律有，

（２）设小球摆到的最高点与最低点相差高度为Ｈ，对全过程运用动能定理有，。

14．解：（１）汽车以正常情况下的最高速度行驶时　的功率是额定功率

这时汽车做的匀速运动，牵引力和阻力大小相等，即Ｆ＝Ｆ_１

设阻力是重力的ｋ倍，Ｆ_１＝ｋｍｇ

代入数据得ｋ＝0.12

（２）设汽车以额定功率行驶速度为时的牵引力为，则，

而阻力大小仍为由代入数据可得ａ＝1.2。

   15．解：（１）设物体Ａ、Ｂ相对于车停止滑动时，车速为v，根据动量守恒定律

方向向右

（２）设物体Ａ、Ｂ在车上相对于车滑动的距离分别为，车长为Ｌ，由功能关系

可知Ｌ至少为6.8ｍ

     16．解：设Ａ、Ｂ系统滑到圆轨道最低点时锁定为，解除弹簧锁定后Ａ、Ｂ的速度分别为，Ｂ到轨道最高点的速度为Ｖ，则有

解得：

17．解：炮弹上升到达最高点的高度为H，根据匀变速直线运动规律，有  v₀²=2gH     

设质量为m的弹片刚爆炸后的速度为V，另一块的速度为v，根据动量守恒定律，

有mV=（M-m）v    

设质量为m的弹片运动的时间为t，根据平抛运动规律，有 H=gt²      R=Vt     

炮弹刚爆炸后，由能量守恒定律可得：两弹片的总动能E_k=mV²+（M－m）v²     

解以上各式得  E_k=＝6.0×10⁴ J