
题目列表(包括答案和解析)
(本小题满分13分)
某种家用电器每台的销售利润与该电器的无故障使用时间![]() (单位:年)有关. 若
(单位:年)有关. 若![]() ,则销售利润为
,则销售利润为![]() 元;若
元;若![]() ,则销售利润为
,则销售利润为![]() 元;若
元;若![]() ,则销售利润为
,则销售利润为![]() 元.设每台该种电器的无故障使用时间
元.设每台该种电器的无故障使用时间![]() ,
,![]() 及
及![]() 这三种情况发生的概率分别为
这三种情况发生的概率分别为![]() ,
,![]() ,
,![]() ,叉知
,叉知![]() ,
,![]() 是方程
是方程![]() 的两个根,且
的两个根,且![]() (1)求
(1)求![]() ,
,![]() ,
,![]() 的值; (2)记
的值; (2)记![]() 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求![]() 的期望.
的期望.
((本小题共13分)
若数列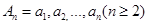 满足
满足 ,数列
,数列 为
为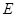 数列,记
数列,记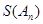 =
= .
.
(Ⅰ)写出一个满足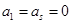 ,且
,且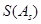 〉0的
〉0的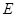 数列
数列 ;
;
(Ⅱ)若 ,n=2000,证明:E数列
,n=2000,证明:E数列 是递增数列的充要条件是
是递增数列的充要条件是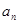 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列 ,使得
,使得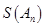 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列 ;如果不存在,说明理由。
;如果不存在,说明理由。
【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(Ⅱ)必要性:因为E数列A5是递增数列,所以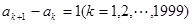 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000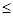 1,a2000—a1000
1,a2000—a1000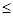 1……a2—a1
1……a2—a1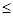 1所以a2000—a
1所以a2000—a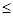 19999,即a2000
19999,即a2000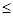 a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故
a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。
(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为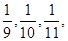 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;(4分)
(2)获赔金额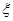 的分别列与期望。(9分)
的分别列与期望。(9分)
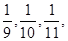 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中: 的分别列与期望。(9分)
的分别列与期望。(9分)(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为![]() 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;
(2)获赔金额![]() 的分别列与期望。
的分别列与期望。
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:(本大题共5个小题,每小题5分,共25分,)
11. 12. 13. 14. 15.
三、解答题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com