1,3,5
三、解答题
(17)解:(Ⅰ) -
---------------------------2分
-
---------------------------2分
高三年级人数为 -------------------------3分
-------------------------3分
现用分层抽样的方法在全校抽取48名学生,应在高三年级抽取的人数为
 (人).
--------------------------------------6分
(人).
--------------------------------------6分
(Ⅱ)设“高三年级女生比男生多”为事件 ,高三年级女生、男生数记为
,高三年级女生、男生数记为 .
.
由(Ⅰ)知 且
且
则基本事件空间包含的基本事件有

 共11个,
------------------------------9分
共11个,
------------------------------9分
事件 包含的基本事件有
包含的基本事件有
 共5个
共5个
 --------------------------------------------------------------11分
--------------------------------------------------------------11分
答:高三年级女生比男生多的概率为 . …………………………………………12分
. …………………………………………12分
(18)解:(Ⅰ) …………2分
…………2分
在 中,由于
中,由于 ,
,
 …………3分
…………3分
又 ,
,

又 ,所以
,所以 ,而
,而 ,因此
,因此 .…………6分
.…………6分
(Ⅱ)由 ,
,
由正弦定理得 …………8分
…………8分
 ,
,
即 ,由(Ⅰ)知
,由(Ⅰ)知 ,所以
,所以 …………10分
…………10分
由余弦弦定理得  , …………11分
, …………11分
 ,
,
 …………12分
…………12分
(19)(Ⅰ)证明:∵ 、
、 分别为
分别为 、
、 的中点,∴
的中点,∴ .
.
又∵ 平面
平面 平面
平面
∴ 平面
平面 …………4分
…………4分
(Ⅱ)∵ ,
, ,∴
,∴
 平面
平面 .
.
又∵ ,∴
,∴
 平面
平面 .
.
∵ 平面
平面 ,∴平面
,∴平面
 平面
平面 .
…………8分
.
…………8分
(Ⅲ)∵
 平面
平面 ,∴
,∴ 是三棱锥
是三棱锥 的高.
的高.
在Rt△ 中,
中, .
.
在Rt△ 中,
中, .
.
∵ ,
, 是
是 的中点,
的中点,
∴ ,
,
故 . ………………12分
. ………………12分
(20)解:(Ⅰ)依题意得
 …………2分
…………2分
解得 ,
…………4分
,
…………4分
 . …………6分
. …………6分
(Ⅱ)由已知得 ,
…………8分
,
…………8分

………………12分
(21)解:(Ⅰ)
令 =0,得
=0,得 ………2分
………2分
因为 ,所以可得下表:
,所以可得下表:


0


+
0
-

ㄊ
极大
ㄋ
………………4分
因此 必为最大值,∴
必为最大值,∴ ,因此
,因此 ,
,
 ,
,
即 ,∴
,∴ ,
,
∴  ……………6分
……………6分
(Ⅱ)∵ ,∴
,∴ 等价于
等价于 , ………8分
, ………8分
令 ,则问题就是
,则问题就是 在
在 上恒成立时,求实数
上恒成立时,求实数 的取值范围,为此只需
的取值范围,为此只需 ,即
,即 ,
…………10分
,
…………10分
解得 ,所以所求实数
,所以所求实数 的取值范围是[0,1].
………………12分
的取值范围是[0,1].
………………12分
(22)解:(Ⅰ)由 得,
得, ,
,
所以直线过定点(3,0),即 .
…………………2分
.
…………………2分
设椭圆 的方程为
的方程为 ,
,
则 ,解得
,解得 ,
,
所以椭圆 的方程为
的方程为 .
……………………5分
.
……………………5分
(Ⅱ)因为点 在椭圆
在椭圆 上运动,所以
上运动,所以 , ………………6分
, ………………6分
从而圆心 到直线
到直线 的距离
的距离

所以直线 与圆
与圆 恒相交.
……………………9分
恒相交.
……………………9分
又直线 被圆
被圆 截得的弦长
截得的弦长
 ,
…………12分
,
…………12分
由于 ,所以
,所以 ,则
,则 ,
,
即直线 被圆
被圆 截得的弦长的取值范围是
截得的弦长的取值范围是 . …………………14分
. …………………14分

![]() x与圆x2+y2+mx+ny-4=0交于M、N两点,且M、N关于直线x+y=0对称,则弦MN的长为
x与圆x2+y2+mx+ny-4=0交于M、N两点,且M、N关于直线x+y=0对称,则弦MN的长为![]() 交于M、N
交于M、N ![]() 为平面区域
为平面区域  内任意一点,则
内任意一点,则![]() 的取值范围是 .
的取值范围是 . 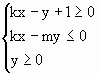 表示的平面区域的面积是
表示的平面区域的面积是 所表示的平面区域的面积是________.
所表示的平面区域的面积是________. 表示的平面区域的面积是
表示的平面区域的面积是![]()
![]()