练习册

  • 练习册
  • 试题
    19 【查看更多】

     

    题目列表(包括答案和解析)

     (19)（本小题满分12分）

    为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物。某人一次种植了n株沙柳，各株沙柳成活与否是相互独立的，成活率为p，设为成活沙柳的株数，数学期望，标准差为。

    （Ⅰ）求n,p的值并写出的分布列；

    （Ⅱ）若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率

    查看答案和解析>>

     19（本小题满分12分）

    P是以为焦点的双曲线C：（a＞0，b＞0）上的一点，已知=0，．

    （1）试求双曲线的离心率；

    （2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当，= 0，求双曲线的方程．

    查看答案和解析>>

     (19) （本小题满分12分）某厂家根据以往的经验得到有关生产销售规律如下：每生产（百台），其总成本为（万元），其中固定成本2万元，每生产1百台需生产成本1万元（总成本固定成本生产成本）；销售收入（万元）满足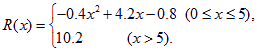：（Ⅰ）要使工厂有盈利，求的取值范围；

    （Ⅱ）求生产多少台时，盈利最多？

    查看答案和解析>>

    （本小题满分12分）

    某初级中学有三个年级，各年级男、女生人数如下表：

    初一年级

    初二年级

    初三年级

    女生

    370

    z

    200

    男生

    380

    370

    300

    已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

       （1）求z的值；

       （2）用分层抽样的方法在初三年级中抽取一个容量为5的样本，将该样本看成一个总体,从中任选2名学生，求至少有1名女生的概率；

       （3）用随机抽样的方法从初二年级女生中选出8人，测量它们的左眼视力，结果如下：1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.1的概率.

    查看答案和解析>>

    （本小题满分12分）

    某初级中学共有学生2000名，各年级男、女生人数如下表：

    初一年级

    初二年级

    初三年级

    女生

    373

    x

    Y

    男生

    377

    370

    z

    已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19。   （I）求x的值；  （II）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？ （III）已知，求初三年级中女生比男生多的概率。

    查看答案和解析>>

    一、1 B     2 D    3 A   4 D     5 C     6 B   

    7 A     8  A   9 C   10 D    11 C    12 B

    二、13、3     14、      15、-160       16、   

    三、17、解: (1)      ……… 3分

         的最小正周期为                     ………………… 5分

    (2)  ,    …………………   7分     

                   ………………… 10分  

                   …………………  11分

     当时,函数的最大值为1,最小值  ……… 12分

    18.解：(1)P1=；                          ……… 6分

    （2）方法一：P2=

    方法二：P2=

    方法三：P2=1-            ……… 12分

    19、解法一：

    （Ⅰ）连结C交BC于O，则O是B C的中点，连结DO。

    ∵在△AC中，O、D均为中点，

    ∴A∥DO…………………………2分

    ∵A平面BD，DO平面BD，

    ∴A∥平面BD。…………………4分

    （Ⅱ）设正三棱柱底面边长为2，则DC = 1。

        ∵∠DC = 60°，∴C= 。

    作DE⊥BC于E。

    ∵平面BC⊥平面ABC，

    ∴DE⊥平面BC

    作EF⊥B于F，连结DF，则 DF⊥B

    ∴∠DFE是二面角D-B-C的平面角………………8分

    在Rt△DEC中，DE=

    在Rt△BFE中，EF = BE?sin

    ∴在Rt△DEF中，tan∠DFE =

    ∴二面角D－B－C的大小为arctan………………12分

    解法二：以AC的中D为原点建立坐标系，如图，

    设| AD | = 1∵∠DC =60°∴| C| = 。

         则A（1，0，0），B（0，，0），C（-1，0，0），

    （1，0）， ，

    （Ⅰ）连结C交B于O是C的中点，连结DO，则     

         O.       =

    ∵A平面BD，

    ∴A∥平面BD.………………………………………………4分

    （Ⅱ）=（-1，0，），

           设平面BD的法向量为n = （ x , y , z ），则

           即  则有= 0令z = 1

    则n = （，0，1）          …………………………………8分

           设平面BC的法向量为m = ( x′ ,y′，z′)

     

    ′

    ′

    ′

    ′

          令y = -1，解得m = （，-1，0）

          二面角D ―B―C的余弦值为cos＜n , m＞＝

    ∴二面角D―B―C的大小为arc cos               …………１２分

    20、解: 解：

         （1）f(x)=x3+ax2+bx+c,    f′(x)=3x2+2ax+b,

             由f′(-)=a+b=0,   f′(1)=3+2a+b=0,得

             a=－，b=－2，…………  ３分

    f′（x）=3x2-x-2=（3x+2）（x-1），函数f（x）的单调区间如下表：

    ｘ

    （-∞，－）

    －

    （－，1）

    1

    （1，+∞）

    f′（x）

    +

    0

    －

    0

    +

    f（x）

     

    ㄊ

    极大值

    ㄋ

    极小值

    ㄊ

    所以函数f（x）的递增区间为（－∞，－）与（1，+∞）；

    递减区间为（－，1）.　　　　　　　　　　　　 …………  ６分

    （2）f（x）=x3-x2-2x+c  x∈［-1，2］，当x=-时，f（x）=+c为极大值，

    而f（2）=2+c，则f（2）=2+c为最大值. 　　　　　…………  ８分

    要使f（x）＜c2（x∈［-1，2］）恒成立，只须c2＞f（2）=2+c，

    解得c＜－1或c＞2. 　　　　　　　　　　　　　　…………  12分

    21、（I）解：方程的两个根为，，

    当时，，所以；

    当时，，，所以；

    当时，，，所以时；

    当时，，，所以．      …………  4分

    （II）解：

    ．                          …………  8分

    （Ⅲ）=                       …………  12分

    22、解： （I）依题意知,点的轨迹是以点为焦点、直线为其相应准线,

    离心率为的椭圆

    设椭圆的长轴长为2a,短轴长为2b,焦距为2c,

    又，，∴点在x轴上,且,且则3

    解之得：,     ∴坐标原点为椭圆的对称中心 

    ∴动点M的轨迹方程为：        …………  4分

    （II）设,设直线的方程为,代入得

                       ………… 5分

    , 

        ………… 6分

    ,,

    ,

     

    解得: (舍)   ∴ 直线EF在X轴上的截距为    …………8分

    （Ⅲ）设,由知, 

    直线的斜率为    ………… 10分

    当时,;

    当时,,

    时取“=”）或时取“=”），

                 ………… 12分            

    综上所述                  ………… 14分 

     


    同步练习册答案