练习册

  • 练习册
  • 试题
    20 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题12分）本某中学为研究学生的身体素质与课外体育锻炼时间的关系，对400名高一学生的一周课外体育锻炼时间进行调查，结果如下表所示：

    锻炼时间（分钟）

    人数

    40

    60

    80

    100

    80

    40

    （1）完成频率分布直方图，并估计该中学高一学生每周参加

    课外体育锻炼时间的平均值（同一组中的数据用该区间的组中值作代表）；

    （2）现采用分层抽样的方法抽取容量为20的样本，

    ①应抽取多少名课外体育锻炼时间为分钟的学生；

    ②若从①中被抽取的学生中随机抽取2名，求这2名学生课外体育锻炼时间均为分钟的概率。

     

    查看答案和解析>>

    （本小题12分）如图，甲船以每小时30海里的速度向正北方向航行，乙船按固定方向匀速直线航行．当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，此时两船相距20海里．当甲船航行20分钟到达A2处时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10海里，问乙船每小时航行多少海里？

     

    查看答案和解析>>

    （本小题12分）某创业投资公司拟投资开发某种新能源产品，估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案：奖金y（单位：万元）随投资收益x（单位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.

    （Ⅰ）若建立函数f(x)模型制定奖励方案，试用数学语言表述公司对奖励函数f(x)模型

    的基本要求；

    （Ⅱ）现有两个奖励函数模型：(i) y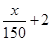＝；(ii) y＝4lgx－3.试分析这两个函数模型

    是否符合公司要求？

     

    查看答案和解析>>

    （本小题12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度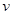（单位：千米/小时）是车流密度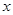（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明；当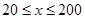时，车流速度v是车流密度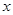的一次函数．

    （Ⅰ）当时，求函数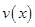的表达式；

    （Ⅱ）当车流密度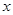为多大时，车流量（单位时间内通过桥上某观点的车辆数，单位：辆/每小时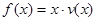）可以达到最大，并求出最大值（精确到1辆/小时）

     

    查看答案和解析>>

    （本小题12分）

    一海轮以20海里/小时的速度向正东航行，它在A点时测得灯塔P在船的北偏东60°方向上，2小时后船到达B点时测得灯塔P在船的北偏东45°方向上。求：

    ①  船在B点时与灯塔P的距离。

    ②  已知以点P为圆心，55海里为半径的圆形水城内有暗礁，那么这船继续向正东航行，有无触礁的危险？

     

     

     

    查看答案和解析>>

    一、1 B     2 D    3 A   4 D     5 C     6 B   

    7 A     8  A   9 C   10 D    11 C    12 B

    二、13、3     14、      15、-160       16、   

    三、17、解: (1)      ……… 3分

         的最小正周期为                     ………………… 5分

    (2)  ,    …………………   7分     

                   ………………… 10分  

                   …………………  11分

     当时,函数的最大值为1,最小值  ……… 12分

    18.解：(1)P1=；                          ……… 6分

    （2）方法一：P2=

    方法二：P2=

    方法三：P2=1-            ……… 12分

    19、解法一：

    （Ⅰ）连结C交BC于O，则O是B C的中点，连结DO。

    ∵在△AC中，O、D均为中点，

    ∴A∥DO…………………………2分

    ∵A平面BD，DO平面BD，

    ∴A∥平面BD。…………………4分

    （Ⅱ）设正三棱柱底面边长为2，则DC = 1。

        ∵∠DC = 60°，∴C= 。

    作DE⊥BC于E。

    ∵平面BC⊥平面ABC，

    ∴DE⊥平面BC

    作EF⊥B于F，连结DF，则 DF⊥B

    ∴∠DFE是二面角D-B-C的平面角………………8分

    在Rt△DEC中，DE=

    在Rt△BFE中，EF = BE?sin

    ∴在Rt△DEF中，tan∠DFE =

    ∴二面角D－B－C的大小为arctan………………12分

    解法二：以AC的中D为原点建立坐标系，如图，

    设| AD | = 1∵∠DC =60°∴| C| = 。

         则A（1，0，0），B（0，，0），C（-1，0，0），

    （1，0）， ，

    （Ⅰ）连结C交B于O是C的中点，连结DO，则     

         O.       =

    ∵A平面BD，

    ∴A∥平面BD.………………………………………………4分

    （Ⅱ）=（-1，0，），

           设平面BD的法向量为n = （ x , y , z ），则

           即  则有= 0令z = 1

    则n = （，0，1）          …………………………………8分

           设平面BC的法向量为m = ( x′ ,y′，z′)

     

    ′

    ′

    ′

    ′

          令y = -1，解得m = （，-1，0）

          二面角D ―B―C的余弦值为cos＜n , m＞＝

    ∴二面角D―B―C的大小为arc cos               …………１２分

    20、解: 解：

         （1）f(x)=x3+ax2+bx+c,    f′(x)=3x2+2ax+b,

             由f′(-)=a+b=0,   f′(1)=3+2a+b=0,得

             a=－，b=－2，…………  ３分

    f′（x）=3x2-x-2=（3x+2）（x-1），函数f（x）的单调区间如下表：

    ｘ

    （-∞，－）

    －

    （－，1）

    1

    （1，+∞）

    f′（x）

    +

    0

    －

    0

    +

    f（x）

     

    ㄊ

    极大值

    ㄋ

    极小值

    ㄊ

    所以函数f（x）的递增区间为（－∞，－）与（1，+∞）；

    递减区间为（－，1）.　　　　　　　　　　　　 …………  ６分

    （2）f（x）=x3-x2-2x+c  x∈［-1，2］，当x=-时，f（x）=+c为极大值，

    而f（2）=2+c，则f（2）=2+c为最大值. 　　　　　…………  ８分

    要使f（x）＜c2（x∈［-1，2］）恒成立，只须c2＞f（2）=2+c，

    解得c＜－1或c＞2. 　　　　　　　　　　　　　　…………  12分

    21、（I）解：方程的两个根为，，

    当时，，所以；

    当时，，，所以；

    当时，，，所以时；

    当时，，，所以．      …………  4分

    （II）解：

    ．                          …………  8分

    （Ⅲ）=                       …………  12分

    22、解： （I）依题意知,点的轨迹是以点为焦点、直线为其相应准线,

    离心率为的椭圆

    设椭圆的长轴长为2a,短轴长为2b,焦距为2c,

    又，，∴点在x轴上,且,且则3

    解之得：,     ∴坐标原点为椭圆的对称中心 

    ∴动点M的轨迹方程为：        …………  4分

    （II）设,设直线的方程为,代入得

                       ………… 5分

    , 

        ………… 6分

    ,,

    ,

     

    解得: (舍)   ∴ 直线EF在X轴上的截距为    …………8分

    （Ⅲ）设,由知, 

    直线的斜率为    ………… 10分

    当时,;

    当时,,

    时取“=”）或时取“=”），

                 ………… 12分            

    综上所述                  ………… 14分 

     


    同步练习册答案