
题目列表(包括答案和解析)
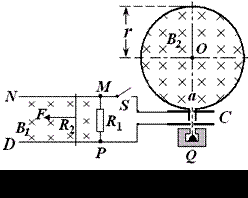
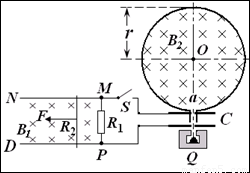
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距l = 0.2m,电阻R1 = 0.4Ω,导轨上静止放置一质量m = 0.1kg、电阻R2 = 0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1 = 0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
(1)5s末时电阻R上消耗的电功率;
(2)5s末时外力F的功率.
(3)若杆最终以8 m/s的速度作匀速运动, 此时闭合电键S,![]() 射线源Q释放的
射线源Q释放的![]() 粒子经加速电场C加速后从a孔对着圆心O进入半径r =
粒子经加速电场C加速后从a孔对着圆心O进入半径r = ![]() m的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场。
m的固定圆筒中(筒壁上的小孔a只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场。![]() 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略![]() 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若![]() 粒子质量
粒子质量![]() = 6.6×10-27 kg , 电量
= 6.6×10-27 kg , 电量![]() = 3.2×10-19 C, 则磁感应强度B2 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
= 3.2×10-19 C, 则磁感应强度B2 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距![]() ,电阻
,电阻![]() ,导轨上静止放置一质量
,导轨上静止放置一质量![]() 、电阻
、电阻![]() 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度![]() 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力![]() 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
(1)5s末时电阻![]() 上消耗的电功率;
上消耗的电功率;
(2)5s末时外力![]() 的功率.
的功率.
(3)若杆最终以8m/s的速度作匀速运动,此时闭合电键S,![]() 射线源Q释放的
射线源Q释放的![]() 粒子经加速电场C加速后从
粒子经加速电场C加速后从![]() 孔对着圆心
孔对着圆心![]() 进入半径
进入半径![]() 的固定圆筒中(筒壁上的小孔
的固定圆筒中(筒壁上的小孔![]() 只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为
只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为![]() 的匀强磁场。
的匀强磁场。![]() 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从![]() 孔背离圆心射出,忽略
孔背离圆心射出,忽略![]() 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若![]() 粒子质量
粒子质量![]() ,电量
,电量![]() ,则磁感应强度
,则磁感应强度![]() 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
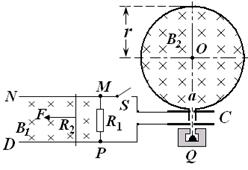
如图所示,光滑且足够长的平行金属导轨![]() 和
和![]() 固定在同一水平面上,两导轨间距,电阻
固定在同一水平面上,两导轨间距,电阻![]() ,导轨上静止放置一质量
,导轨上静止放置一质量![]() 、电阻
、电阻![]() 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度![]() 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力![]() 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求:
(1)5s末时电阻![]() 上消耗的电功率;
上消耗的电功率;
(2)金属杆在5s末的运动速率;
(3)5s末时外力![]() 的功率.
的功率.

如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距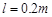 ,电阻
,电阻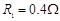 ,导轨上静止放置一质量
,导轨上静止放置一质量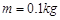 、电阻
、电阻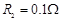 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度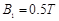 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力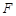 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
(1)5s末时电阻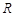 上消耗的电功率;
上消耗的电功率;
(2)5s末时外力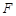 的功率.
的功率.
(3)若杆最终以8m/s的速度作匀速运动,此时闭合电键S,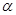 射线源Q释放的
射线源Q释放的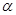 粒子经加速电场C加速后从
粒子经加速电场C加速后从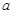 孔对着圆心
孔对着圆心 进入半径
进入半径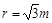 的固定圆筒中(筒壁上的小孔
的固定圆筒中(筒壁上的小孔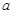 只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为
只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为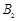 的匀强磁场。
的匀强磁场。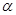 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从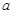 孔背离圆心射出,忽略
孔背离圆心射出,忽略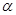 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若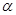 粒子质量
粒子质量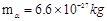 ,电量
,电量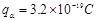 ,则磁感应强度
,则磁感应强度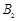 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距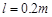 ,电阻
,电阻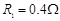 ,导轨上静止放置一质量
,导轨上静止放置一质量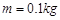 、电阻
、电阻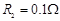 的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度
的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度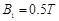 的匀强磁场中,磁场的方向竖直向下,现用一外力
的匀强磁场中,磁场的方向竖直向下,现用一外力 沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
(1)5s末时电阻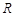 上消耗的电功率;
上消耗的电功率;
(2)5s末时外力 的功率.
的功率.
(3)若杆最终以8m/s的速度作匀速运动,此时闭合电键S,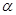 射线源Q释放的
射线源Q释放的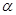 粒子经加速电场C加速后从
粒子经加速电场C加速后从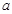 孔对着圆心
孔对着圆心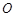 进入半径
进入半径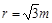 的固定圆筒中(筒壁上的小孔
的固定圆筒中(筒壁上的小孔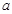 只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为
只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为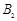 的匀强磁场。
的匀强磁场。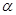 粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从
粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失,粒子与圆筒壁碰撞5次后恰又从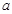 孔背离圆心射出,忽略
孔背离圆心射出,忽略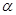 粒子进入加速电场的初速度,若
粒子进入加速电场的初速度,若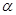 粒子质量
粒子质量 ,电量
,电量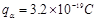 ,则磁感应强度
,则磁感应强度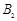 多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
多大?若不计碰撞时间,粒子在圆筒内运动的总时间多大?
班级 姓名 学号
一、二、选择题:
1
2
3
4
5
6
7
8
9
D
C
D
B
D
AD
BC
AD
ABD
三、填空题:
10、(8分)⑴20.30 ⑵①S1/2T;② 9.71~9.73 ③阻力作用 (每空2分)
11、.files/image077.gif) (12分)①B;D;F (每空1分,共3分)
(12分)①B;D;F (每空1分,共3分)
.files/image079.jpg) ② (4分)
③ (3分)
② (4分)
③ (3分)
④变大 (2分)
12、(10分)(1)E 3分
(2)此波向右传播 2分
波速.files/image081.gif) 3分
3分
1.0秒内b质点通过的路程是.files/image083.gif) 2分
2分
四、计算题:
13、(12分)(1)由于小孩无碰撞进入圆弧轨道,即小孩落到A点时速度方向沿A点切线方向,则
.files/image085.gif) (1分)
(1分)
又由.files/image087.gif) (2分)
(2分)
而.files/image089.gif) (1分)
(1分)
联立以上各式得.files/image091.gif) (2分)
(2分)
(2)设小孩到最低点的速度为v,由机械能守恒,有
.files/image093.gif) (2分)
(2分)
在最低点,据牛顿第二定律,有.files/image095.gif) (2 分)
(2 分)
代入数据解得FN=1290N(1分)
由牛顿第三定律可知,小孩对轨道的压力为1290N. (1分)
14、(13分)(1).files/image097.gif) (2分)
(2分)
(2).files/image099.gif) (2分)
(2分)
.files/image101.gif) (2分)
(2分)
U=IR(1分)
由以上各式得v=2.5m/s(1分)
(3)金属棒加速度.files/image103.gif) (1分)
(1分)
由牛顿定律.files/image105.gif) (2分)
(2分)
.files/image107.gif)
由以上各式得P=0.25W(1分)
15、(17分)
.files/image109.jpg)
g
16、(17分)(1)I、III区域中.files/image111.gif) (2分)
(2分)
.files/image113.gif) (1分)
(1分)
在II区域的电磁场中运动满足
.files/image115.gif) (2分)
(2分)
.files/image117.gif) (1分)
(1分)
方向水平向右(1分)
同理E2=2×103V/m方向水平向左.(1分)
(2)根据对称性,在区域III中只能存在匀强磁场,且满足B3=B2=0.1T,方向垂直纸面向外. (2分)
由于周期相等,所以在区域II中只能存在匀强电场,且方向必须与x轴平行,(2分)
从B点运动至O点做类平抛运动,时间.files/image119.gif) (1分)
(1分)
沿y轴方向的位移是L,则.files/image121.gif) (1分)
(1分)
由牛顿第二定律qE=ma(1分)
代入数据解得E=2×103V/m(1分)
根据
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com