已知函数在取得极值

（1）求的单调区间（用表示）；

（2）设，，若存在，使得成立，求的取值范围.

【解析】第一问利用

根据题意在取得极值,

对参数a分情况讨论，可知

当即时递增区间:    递减区间: ,

当即时递增区间:    递减区间: ,

第二问中， 由(1)知: 在，

，

在 

从而求解。

解:

…..3分

在取得极值, ……………………..4分

(1) 当即时  递增区间:    递减区间: ,

当即时递增区间:    递减区间: , ………….6分

 (2)  由(1)知: 在，

，

在 

……………….10分

, 使成立

    得:

 

 （由理科第三册§1.3P18习题1.2第1题改编）某工厂规定，如果工人在一个季度里有一个月完成生产任务，可得奖金90元；如果有2个月完成生产任务，可得奖金210元；如果有3个月完成生产任务，可得奖金330元；如果3个月都未完成任务，则没有奖金．已知某工人每个月完成生产任务的概率都是75%.

⑴求这个工人在连续三个季度里恰有两个季度未获得奖金的概率;

⑵求这个工人在一个季度里所得奖金的期望（精确到元）．

 

 

 

 

 

 

 

(09全国2文1)已知全集U={1，2，3，4，5，6，7，8}，M={1，3，5，7}，N={5，6，7}，则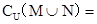

A .{5，7}            B. {2，4}            C.{2,4,8}         D. {1,3,5,7}

 

已知函数f(x)=x²+1，x∈R.

(1)分别计算f(1)-f(-1)，f(2)-f(-2)，f(3)-f(-3)的值.

(2)由(1)你发现了什么结论？并加以证明.

(1)已知抛物线y²=2px(p＞0),过焦点F的动直线l交抛物线于A、B两点,O为坐标原点,求证: ·为定值;

(2)由(1)可知:过抛物线的焦点F的动直线l交抛物线于A、B两点,存在定点P,使得PA·PB为定值.请写出关于椭圆的类似结论,并给出证明.