练习册

  • 练习册
  • 试题
    (2) 求证:. 得 分评卷人 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数fn（x）=（1+x）n-1，（n∈N*，且n＞1）．
    （1）设函数h（x）=f3（x）-F2（x），x∈[-2，0]，求h（x）的最大值和最小值．
    （2）若x＞-2求证：fn（x）≥nx．

    查看答案和解析>>

    用反证法证明：若x，y都是正实数，且x+y＞2求证：
    1+x
    y
    ＜2    或
    1+y
    x
    ＜2    中至少有一个成立．

    查看答案和解析>>

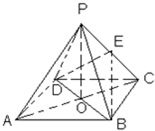    精英家教网如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．PO=
    		2
    ，AB=2
    求证：（1）PA∥平面BDE
    （2）平面PAC⊥平面BDE
    （3）求二面角E-BD-A的大小．

    查看答案和解析>>

    设a＞2，给定数列{xn}，其中x1=a，xn+1=
    x
    2
    n
    2(xn-1)
    (n=1，2…)    求证：
    （1）xn＞2，且
    xn+1
    xn
    ＜1(n=1，2…)    ；
    （2）如果a≤3，那么xn≤2+
    1
    2n-1
    (n=1，2…)    ．

    查看答案和解析>>

    (本小题满分16分)

    已知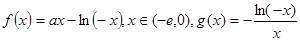，其中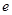是自然常数，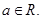

     (1)讨论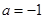时, 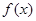的单调性、极值；

     (2)求证：在（1）的条件下，；

     (3)是否存在实数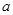，使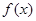的最小值是3，如果存在，求出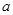的值；如果不存在，说明理由.

     

    查看答案和解析>>

    一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。

    1．B  2．D 3．B  4．C  5．C  6．B  7．A  8．B  9．A  10．D

     

    二、填空题：本大题共5个小题，每小题5分，共25分，把答案填在题中的横线上。

    11.6  12．2   13．80  14．20  15． 0，

    三、解答题：本大题共6小题，共75分。解答应写文字说明，证明过程或演算步骤。

    16．解(1)证明:由得

    ∴………………………………………………4分

    (2)由正弦定理得     ∴……① …………6分

      又,=2,       ∴ …………② …………8分

    解①②得 ,           …………………………………………10分

    ∴                          …………………12分

    17．解:(1)由得,即=0.……………2分

    当n>2时有

       ∴                        ……………………………6分

    (2)由(1)知n>2时,……………8分

    又=0,  =2也适合上式,

    ∴   ∴……………………10分

    ∴

                      =1-<1……………………………………………12分

     

    18．解：（1）分别取BE、AB的中点M、N，

    连结PM、MC，PN、NC,则PM=1，MB=，BC=，

    ∴MC=，而PN=MB=，

    NC=，∴PC=，…………………………4分

    ∴

    故所求PC与AB所成角的余弦值为………6分

    （2）连结AP，∵二面角E-AB-C是直二面角，且AC⊥AB

    ∴∠BAP即为所求二面角的平面角，即∠BAP=300……8分

    在RtΔBAF中，tan∠ABF=，∴∠ABF=600，

    故BF⊥AP，    ………………………………………10分

    又AC⊥面BF，∴BF⊥AC，故BF⊥平面PAC………12分

    另解：分别以AB、AC、AF为x、y、z轴建立直角坐标系，

    则，

      ∴

    而，  ∴

    故异面直线PC与AB所成的角的余弦值为

    （2）分别设平面ABC和平面PAC的法向量分别为，P点坐标设为，则而，则由

    得

    且 ∴，

    再由得

    ∴，，

    而

    ∴，即

    BF⊥AP，BF⊥AC∴BF⊥平面PAC

     

    19．解：（1）当0<x≤10时，……2分

    当x >10时，…………4分

    …………………………………5分

    （2）①当0<x≤10时，由

    当

    ∴当x=9时，W取最大值，且……9分

    ②当x>10时，W=98

    当且仅当…………………………12分

    综合①、②知x=9时，W取最大值.

    所以当年产量为9千件时，该公司在这一品牌服装生产中获利最大.……13分

    20． 解: （I） ,依题意有:,…………………2分

                即,

             ,由

              (也可写成闭区间)……………4分

    （2）   (1)

         函数的图象与直线的交点的个数问题可转化为方程(1)的解的个数问题.

           令

    则…………………………5分

    ①6分

    ②

     

       ……………………9分

    ③

    ∴的极大值为

    ∴的图象与轴只有一个交点.…………………………………12分

    综上所述: ;

    .……………13分

     

    21．解：（1）B（0，-b）

    ,即D为线段FP的中点.

    ∴ ……………………………2分

    ,即A、B、D共线.

    而 

    ∴,得,

    ∴………………………………………5分

     

    （2）∵=2,而,∴,故双曲线的方程为………①

    ∴B、的坐标为(0,-1)…………………………………………………………6分

    假设存在定点C（0，）使为常数.

    设MN的方程为………………②

    ②代入①得………………………………………7分

    由题意得:   得:……8分

    设M、N的坐标分别为(x1,y1) 、(x2,y2)

         …………………………………………………………9分

    而=

             =

    ==,…………………………10分

    整理得:

    对满足的恒成立.

    ∴且

    解得

    存在轴上的定点C(0,4),使为常数17.…………………………13分

     

     


    同步练习册答案