
题目列表(包括答案和解析)
已知向量 =(
=( ),
), =(
=(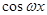 ,
,
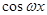 ),其中(
),其中(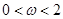 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得 ,……11分故
,……11分故
已知正四棱柱 中,
中, .
.
(1)求证: ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)在线段 上是否存在点
上是否存在点 ,使得平面
,使得平面
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
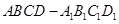 中,
中,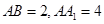 .
. 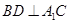 ;
;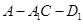 的余弦值;
的余弦值;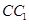 上是否存在点
上是否存在点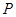 ,使得平面
,使得平面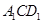
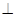 平面
平面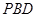 ,若存在,求出
,若存在,求出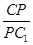 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.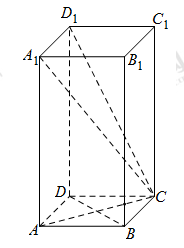
如图,在三棱锥 中,
中,  ,
,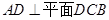 ,
,

 为线段
为线段 的中点.
的中点.
(Ⅰ)求证: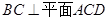 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.

如图,在几何体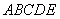 中,
中, ,
,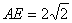 ,
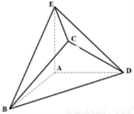
,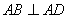 ,且
,且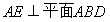 ,
,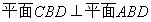 .
.
(I)求证: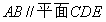 ;
;
(II)求二面角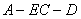 的余弦值.
的余弦值.
一.选择题:CCBAB BBADA
解析:1:由映射概念可知 可得
可得 .故选
.故选 .
.
2:如图, +3
+3 =
= ,在
,在 中,
中, 由余弦定理得|
由余弦定理得| +3
+3 |=|
|=| |=
|= ,故选C。
,故选C。
3:取 ,由图象可知,此时注水量
,由图象可知,此时注水量 大于容器容积的
大于容器容积的 ,故选B。
,故选B。
4:因 为三角形中的最小内角,故
为三角形中的最小内角,故 ,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
5:取x=4,y=?100%≈-8.3%,排除C、D;取x=30,y = ?100%≈77.2%,排除A,故选B。
 6:等差数列的前n项和Sn=
6:等差数列的前n项和Sn= n2+(a1-
n2+(a1- )n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n=
)n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n= ,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。
,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。
7:∵A,B是一对矛盾命题,故必有一真,从而排除错误支C,D。又由ab<0,可令a=1,b= -1,代入知B为真,故选B。
8:借助立体几何的两个熟知的结论:(1)一个正方体可以内接一个正四面体;(2)若正方体的顶点都在一个球面上,则正方体的对角线就是球的直径。可以快速算出球的半径 ,从而求出球的表面积为
,从而求出球的表面积为 ,故选A。
,故选A。
9:分析选择支可知,四条曲线中有且只有一条曲线不符合要求,故可考虑找不符合条件的曲线从而筛选,而在四条曲线中②是一个面积最大的椭圆,故可先看②,显然直线和曲线 是相交的,因为直线上的点
是相交的,因为直线上的点 在椭圆内,对照选项故选D。
在椭圆内,对照选项故选D。
10: ,从而对任意的
,从而对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 为常数。充分利用题中给出的常数10,100。令
为常数。充分利用题中给出的常数10,100。令 ,当
,当 时,
时, ,由此得
,由此得 故选A。
故选A。
二.填空题:11、 ; 12、
; 12、 ; 13、
; 13、 ;
;
14、 ; 15、
; 15、 ;
;
解析:11:不等式 等价于
等价于 ,也就是
,也就是 ,所以
,所以 ,从而应填
,从而应填 .
.
12:  ,不论
,不论 的值如何,
的值如何, 与
与 同号,所以
同号,所以
13:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆 的圆心的距离不超过半径,∴
的圆心的距离不超过半径,∴ 。
。
14.解:由正弦定理得 即
即 ,∴所求直线的极坐标方程为
,∴所求直线的极坐标方程为 .
.
15.解: 即
即 ,
,

三.解答题:
16.解:(Ⅰ)函数  要有意义需满足:
要有意义需满足: 即
即 ,解得
,解得 ,
, …………………………………3分
…………………………………3分
函数 要有意义需满足
要有意义需满足 ,即
,即 ,
,
解得 或
或
 …………………………………6分
…………………………………6分
(Ⅱ)由(Ⅰ)可知 ,
, ,
,
 ,
, ………………………12分
………………………12分
17.解:(I)因为 是等比数列,
是等比数列,
又 …………………………………………2分
…………………………………………2分

∴ 是以a为首项,
是以a为首项, 为公比的等比数列.………………………………6分
为公比的等比数列.………………………………6分
(II)(I)中命题的逆命题是:若 是等比数列,则
是等比数列,则 也是等比数列,是假命题.
也是等比数列,是假命题.
……………………………………………………………8分
设 的公比为
的公比为 则
则
又
 是以1为首项,q为公比的等比数列,
是以1为首项,q为公比的等比数列,
 是以
是以 为首项,q为公比的等比数列.……………………10分
为首项,q为公比的等比数列.……………………10分
即 为1,a,q,aq,q2,aq2,…
为1,a,q,aq,q2,aq2,…
但当q≠a2时, 不是等比数列
不是等比数列
故逆命题是假命题.……………………………………………………………………12分
另解:取a=2,q=1时,

因此 是等比数列,而
是等比数列,而 不是等比数列.
不是等比数列.
故逆命题是假命题.……………………………………………………………………12分
18.解:(1)设选对一道“可判断2个选项是错误的”题目为事件A,“可判断1个选项是错误的”该题选对为事件B,“不能理解题意的”该题选对为事件C.则 ---
---
所以得40分的概率 ………………………………4分
………………………………4分
(2) 该考生得20分的概率 =
= ……………………5分
……………………5分
该考生得25分的概率:

= ……………………6分
……………………6分
该考生得30分的概率: =
= =
=  --------------7分
--------------7分
该考生得35分的概率:

= ……………………9分
……………………9分
∵ ∴该考生得25分或30分的可能性最大………………………………11分
∴该考生得25分或30分的可能性最大………………………………11分
(3)该考生所得分数的数学期望 =
=
………………………………14分
19.解:(Ⅰ)由 知圆心C的坐标为
知圆心C的坐标为 --------------(1分)
--------------(1分)
∵圆C关于直线 对称
对称
∴点 在直线
在直线 上 -----------------(2分)
上 -----------------(2分)
即D+E=-2,------------①且 -----------------②-----------------(3分)
-----------------②-----------------(3分)
又∵圆心C在第二象限 ∴ -----------------(4分)
-----------------(4分)
由①②解得D=2,E=-4 -----------------(5分)
∴所求圆C的方程为: ------------------(6分)
------------------(6分)
(Ⅱ) 切线在两坐标轴上的截距相等且不为零,设
切线在两坐标轴上的截距相等且不为零,设 :
: -----------(7分)
-----------(7分)
 圆C:
圆C:
 圆心
圆心 到切线的距离等于半径
到切线的距离等于半径 ,
,
即
 。
------------------(12分)
。
------------------(12分)
所求切线方程 ------------------(14分)
------------------(14分)
20.(Ⅰ)证明:在正方体 中,∵平面
中,∵平面 ∥平面
∥平面
平面
 平面
平面
 ,平面
,平面
 平面
平面

 ∴
∴ ∥
∥ .-------------------------------------3分
.-------------------------------------3分
(Ⅱ)解:如图,以D为原点分别以DA、DC、DD1为
x、y、z轴,建立空间直角坐标系,则有
D1(0,0,2),E(2,1,2),F(0,2,1),
∴ ,
,
设平面 的法向量为
的法向量为 
则由 ,和
,和 ,得
,得 ,
,
取 ,得
,得 ,
, ,∴
,∴ ------------------------------6分
------------------------------6分
又平面 的法向量为
的法向量为 (0,0,2)
(0,0,2)
故 ;
;
∴截面 与底面
与底面 所成二面角的余弦值为
所成二面角的余弦值为 . ------------------9分
. ------------------9分
(Ⅲ)解:设所求几何体 的体积为V,
的体积为V,
∵ ~
~ ,
, ,
, ,
,
∴ ,
, ,
,
∴ ,
,
 --------------------------11分
--------------------------11分
故V棱台


∴V=V正方体-V棱台
 . ------------------14分
. ------------------14分
21.解:(Ⅰ)由题意, 在[
在[ ]上递减,则
]上递减,则 解得
解得
所以,所求的区间为[-1,1] ………………………4分
(Ⅱ)取 则
则 ,即
,即 不是
不是 上的减函数。
上的减函数。
取
 ,
,
即 不是
不是 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。-------9分
(Ⅲ)若 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数 的值域为[
的值域为[ ],即
],即 ,
, 为方程
为方程 的两个实数根,
的两个实数根,
即方程 有两个不等的实根。
有两个不等的实根。
当 时,有
时,有 ,解得
,解得 。
。
当 时,有
时,有 ,无解。
,无解。
综上所述, ---------------------------------------------14分
---------------------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com