
题目列表(包括答案和解析)
A)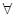 n∈N,2n≤1000 (B)
n∈N,2n≤1000 (B)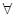 n∈N,2n>1000
n∈N,2n>1000
(C)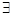 n∈N,2n≤1000 (D)
n∈N,2n≤1000 (D)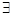 n∈N,2n<1000
n∈N,2n<1000
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
| π |
| 6 |
| 1 |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
一.选择题:DCDDA DDBBC
解析:1:复数i的一个辐角为900,利用立方根的几何意义知,另两个立方根的辐角分别是900+1200与900+2400,即2100与3300,故虚部都小于0,答案为(D)。
2:把x=3代入不等式组验算得x=3是不等式组的解,则排除(A)、(B), 再把x=2代入不等式组验算得x=2是不等式组的解,则排除(D),所以选(C).
3:在题设条件中的等式是关于 与
与 的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有
的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有 ,即
,即 ,从而C被淘汰,故选D。
,从而C被淘汰,故选D。
4:“对任意的x1、x2,当 时,
时, ”实质上就是“函数单调递减”的“伪装”,同时还隐含了“
”实质上就是“函数单调递减”的“伪装”,同时还隐含了“ 有意义”。事实上由于
有意义”。事实上由于 在
在 时递减,从而
时递减,从而 由此得a的取值范围为
由此得a的取值范围为 。故选D。
。故选D。
5:由韦达定理知
.从而 ,故
,故 故选A。
故选A。
6:当点A为切点时,所求的切线方程为 ,当A点不是切点时,所求的切线方程为
,当A点不是切点时,所求的切线方程为 故选D。
故选D。
7:由已知条件可知,EF∥平面ABCD,则F到平面ABCD的距离为2, ∴VF-ABCD= ?32?2=6,而该多面体的体积必大于6,故选(D).
?32?2=6,而该多面体的体积必大于6,故选(D).
8:由二项展开式系数的性质有C +C
+C +…+C
+…+C +C
+C =2
=2 ,选B.
,选B.
9:取特殊数列 =3,则
=3,则 =
= =10,选(B).
=10,选(B).
10:本题是考查双曲线渐近线夹角与离心率的一个关系式,故可用特殊方程来考察。取双曲线方程为 -
- =1,易得离心率e=
=1,易得离心率e= ,cos
,cos =
= ,故选C。
,故选C。
二.填空题:11、 ; 12、
; 12、 ;13、
;13、 ;14、
;14、 ,
, ;15、
;15、 ,
, ;
;
解析:11:因为 (定值),于是
(定值),于是 ,
, ,
, ,又
,又 , 故原式=
, 故原式= 。
。
12:因为正方形的面积是16,内切圆的面积是 ,所以豆子落入圆内的概率是
,所以豆子落入圆内的概率是 .
.
13:设k = 0,因抛物线焦点坐标为 把直线方程
把直线方程 代入抛物线方程得
代入抛物线方程得 ,∴
,∴ ,从而
,从而 。
。
14.(略)
15.(略)
三.解答题:
16.解:(1)∵对任意 ,
, ,∴
,∴ --2分
--2分
∵ 不恒等于
不恒等于 ,∴
,∴ --------------------------4分
--------------------------4分
(2)设
① 时,由
时,由 解得:
解得:
由 解得其反函数为
解得其反函数为  ,
, -----------------7分
-----------------7分
② 时,由
时,由 解得:
解得:
解得函数 的反函数为
的反函数为 ,
, --------------------9分
--------------------9分
∵
∴ ------------------------------------------------------------------12分
------------------------------------------------------------------12分
17.解:(Ⅰ)依题意,有
 ,
, .
.
因此, 的解析式为
的解析式为 ; …………………6分
; …………………6分
(Ⅱ)由 (
( )得
)得 (
( ),解之得
),解之得
 (
( )
)
由此可得
 且
且 ,
,
所以实数 的取值范围是
的取值范围是 . …………………12分
. …………………12分
18.(I)因为侧面 是圆柱的的轴截面,
是圆柱的的轴截面, 是圆柱底面圆周上不与
是圆柱底面圆周上不与 、
、 重合一个点,所以
重合一个点,所以 …………………2分
…………………2分
 又圆柱母线
又圆柱母线 ^平面
^平面 ,
, Ì平面
Ì平面 ,所以
,所以 ^
^ ,
,
又

 ,所以
,所以 ^平面
^平面 ,
,
因为 Ì平面
Ì平面 ,所以平面
,所以平面
 平面
平面 ;…………………………………6分
;…………………………………6分
(II)设圆柱的底面半径为 ,母线长度为
,母线长度为 ,
,
当点 是弧
是弧 的中点时,三角形
的中点时,三角形 的面积为
的面积为 ,
,
三棱柱 的体积为
的体积为 ,三棱锥
,三棱锥 的体积为
的体积为 ,
,
四棱锥 的体积为
的体积为 ,………………………………………10分
,………………………………………10分
圆柱的体积为 ,
………………………………………………12分
,
………………………………………………12分
四棱锥 与圆柱的体积比为
与圆柱的体积比为 .……………………………………………14分
.……………………………………………14分
19.(Ⅰ)解:∵
∴

∴数列 是首项为(
是首项为( ),公比为2的等比数列,………………4分
),公比为2的等比数列,………………4分
 ,
,


 ,∴数列
,∴数列 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
 ,∴
,∴ …
…………………7分
…
…………………7分
(Ⅱ)令 代入
代入 得:
得:
 解得:
解得:
由此可猜想 ,即
,即 …………………10分
…………………10分
下面用数学归纳法证明:
(1)当n=1时,等式左边=1,右边= ,
,
 当n=1时,等式成立,
当n=1时,等式成立,
(2)假设当n=k时,等式成立,即
当n=k+1时





∴当n=k+1时,等式成立,
综上所述,存在等差数列 ,使得对任意的
,使得对任意的 有
有 成立。
…………………14分
成立。
…………………14分
20.解:(Ⅰ)∵ 轴,∴
轴,∴ ,由椭圆的定义得:
,由椭圆的定义得: , ……………2分
, ……………2分
∵ ,∴
,∴ ,
,
又 得
得 ∴
∴

 ………………4分
………………4分
∴ ,∴所求椭圆C的方程为
,∴所求椭圆C的方程为 . …………………6分
. …………………6分
(Ⅱ)由(Ⅰ)知点A(-2,0),点B为(0,-1),设点P的坐标为
则 ,
, , 由
, 由 -4得-
-4得- ,
,
∴点P的轨迹方程为 …………………8分
…………………8分
设点B关于P的轨迹的对称点为 ,则由轴对称的性质可得:
,则由轴对称的性质可得: ,
,
解得: ,…………………10分
,…………………10分
∵点 在椭圆上,
在椭圆上,
∴  ,
,
整理得 解得
解得 或
或  …………………12分
…………………12分
∴点P的轨迹方程为 或
或 ,经检验
,经检验 和
和 都符合题设,
都符合题设,
∴满足条件的点P的轨迹方程为 或
或 .…………………14分
.…………………14分
21.解(1) 
 …………………1分
…………………1分
 ,
,
当 时
时 ,函数
,函数 有一个零点;
有一个零点;
当 时,
时, ,函数
,函数 有两个零点。…………………3分
有两个零点。…………………3分
(2)令 ,则
,则

 ,…………………5分
,…………………5分

 在
在 内必有一个实根。即
内必有一个实根。即 ,使
,使 成立。…………………8分
成立。…………………8分
(3)
假设 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且
∴

 ………………10分
………………10分
由②知对 ,都有
,都有
令 得
得



由 得
得 , …………………12分
, …………………12分
当 时,
时, ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
 对
对 ,都有
,都有 ,满足条件②。
,满足条件②。
∴存在 ,使
,使 同时满足条件①、②。 …………………14分
同时满足条件①、②。 …………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com