
题目列表(包括答案和解析)
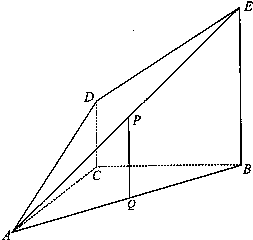
 如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,
如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,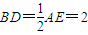 ,O、M分别为CE、AB的中点.
,O、M分别为CE、AB的中点.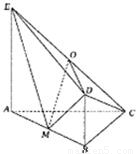

 ,O、M分别为CE、AB的中点.
,O、M分别为CE、AB的中点.
 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.一.选择题:DDCAB DDDAB
解析:1: ∵
∵ ,
,
∴
∴ ,
,
而i,j为互相垂直的单位向量,故可得 ∴
∴ 。故选
。故选
2:∵ ∴0<b<a<1. 由指数函数的单调性可知:
∴0<b<a<1. 由指数函数的单调性可知: ,又∵
,又∵ ∴选(D)
∴选(D)
3:作y= 与y=
与y= 的图象,从图中可以看出:两曲线有3个交点,即方程有3个实根.选(C)
的图象,从图中可以看出:两曲线有3个交点,即方程有3个实根.选(C)
 |
4:由斜率去筛选,则可排除(C)、(D);再用点(-1,3)去筛选,代入(A)成立,
∴应选(A).
5:取α= ± 、±
、± ,代入求出sinα、tanα
、cotα 的值,易知α=-
,代入求出sinα、tanα
、cotα 的值,易知α=- 适合题设条件,∴应选(B).
适合题设条件,∴应选(B).

M - i
2 


6:由复数模的几何意义,画出右图,可知当圆上的点到M的距离最大时即为|z-i|最大。所以选D
7: ∵球的半径R不小于△ABC的外接圆半径r= , 则S球=4πR2≥4πr2=
, 则S球=4πR2≥4πr2= π>5π,故选(D).
π>5π,故选(D).
8:当θ 0时,sin(sinθ)
0时,sin(sinθ) 0,cosθ
0,cosθ 1,cos(cosθ)
1,cos(cosθ) cos1,故排除A,B.
cos1,故排除A,B.
当θ
 时,cos(sinθ)
时,cos(sinθ) cos1,cosθ
cos1,cosθ 0,故排除C,因此选D.
0,故排除C,因此选D.
9:由于 的含义是
的含义是 于是若
于是若 成立,则有
成立,则有 成立;同理,若
成立;同理,若 成立,则
成立,则 也成立,以上与指令“供选择的答案中只有一个正确”相矛盾,故排除
也成立,以上与指令“供选择的答案中只有一个正确”相矛盾,故排除 .再考虑
.再考虑 ,取
,取 代入得
代入得 ,显然
,显然 ,排除
,排除 .故选
.故选 .
.
10:选项暗示我们,只要判断出直线的条数就行,无须具体求出直线方程。以A(1,2)为圆心,1为半径作圆A,以B(3,1)为圆心,2为半径作圆B。由平面几何知识易知,满足题意的直线是两圆的公切线,而两圆的位置关系是相交,只有两条公切线。故选B。
二.填空题:11、 ;12、
;12、 ; 13、
; 13、 或
或 ;14、-1;15、4,
;14、-1;15、4, ;
;
解析:
11:  ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是 ,应填
,应填 .
.
12:容易发现 ,于是 原式=
,于是 原式= ,应填
,应填
13:记椭圆的二焦点为 ,有
,有
则知
显然当 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填 或
或
14.(略)
15.(略)
三.解答题:
16.解:(1)由题设,得
 -----------------3分
-----------------3分
因为 与
与 垂直
垂直  即
即
 . 又
. 又 ,故
,故 ,∴
,∴ 的值为2. ------------------6分
的值为2. ------------------6分
(2)当 垂直时,
垂直时,
 ------------------8分
------------------8分
 ,则
,则 ------------------10分
------------------10分
 ------------------12分
------------------12分
17.解:(I)基本事件总数为 ,
,
若使方程有实根,则 ,即
,即 。------------------2分
。------------------2分
当 时,
时, ; 当
; 当 时,
时, ; ------------------3分
; ------------------3分
当 时,
时, ; 当
; 当 时,
时, ; ------------------4分
; ------------------4分
当 时,
时, ; 当
; 当 时,
时, , ------------------5分
, ------------------5分
目标事件个数为
因此方程 有实根的概率为
有实根的概率为 ------------------6分
------------------6分
(II)由题意知, ,则
,则
 ,
,
 ,
,
故 的分布列为
的分布列为

0
1
2
P



 的数学期望
的数学期望 ------------------10分
------------------10分
(III)记“先后两次出现的点数中有 有实根” 为事件N,则
有实根” 为事件N,则 ,
, ,
,  .------------------12分
.------------------12分

18.解:(Ⅰ) ,
,
由题意得, 是
是 的两个根,
的两个根,
解得, . ------------------2分
. ------------------2分
再由 可得
可得 .
.
∴ . ------------------4分
. ------------------4分
(Ⅱ) ,
,
当 时,
时, ;当
;当 时,
时, ;------------------5分
;------------------5分
当 时,
时, ;当
;当 时,
时, ;------------------6分
;------------------6分
当 时,
时, .∴函数
.∴函数 在区间
在区间 上是增函数;------------------7分
上是增函数;------------------7分
在区间 上是减函数;在区间
上是减函数;在区间 上是增函数.
上是增函数.
函数 的极大值是
的极大值是 ,极小值是
,极小值是 . ------------------9分
. ------------------9分
(Ⅲ)函数 的图象是由
的图象是由 的图象向右平移
的图象向右平移 个单位,向上平移4
个单位,向上平移4 个单位得到,
个单位得到,
所以,函数 在区间
在区间 上的值域为
上的值域为 (
( ).-------------10分
).-------------10分
而 ,∴
,∴ ,即
,即 .
.
于是,函数 在区间
在区间 上的值域为
上的值域为 .------------------12分
.------------------12分
令 得
得 或
或 .
.
由 的单调性知,
的单调性知, ,即
,即 .
.
综上所述, 、
、 应满足的条件是:
应满足的条件是: ,且
,且 ------------------14分
------------------14分
19.(Ⅰ)证明:连结 交
交 于
于 ,连结
,连结 .
.
 是正方形,∴
是正方形,∴  是
是 的中点. ----------1分
的中点. ----------1分
 是
是 的中点, ∴
的中点, ∴ 是
是 的中位线. ∴
的中位线. ∴ . ----------2分
. ----------2分
又∵ 平面
平面 ,
, 
 平面
平面 , ----------3分
, ----------3分
∴
 平面
平面 .------------------4分
.------------------4分
(II)如图,以A为坐标原点,建立空间直角坐标系 ,
,
由 故设
故设 ,则
,则

 . ----------6分
. ----------6分

 底面
底面 ,
,
∴ 是平面
是平面 的法向量,
的法向量, .----------7分
.----------7分
设平面 的法向量为
的法向量为 ,
,
 ,
,
则 即
即
∴  令
令 ,则
,则 . ----------9分
. ----------9分
∴ ,
,
∴二面角 的余弦值为
的余弦值为 . ------------------10分
. ------------------10分
(III)
 ,
,  ,
,
 ----------11分
----------11分
 又
又 且
且 .----------12分
.----------12分
 . 又
. 又 平面
平面 ----------13分
----------13分
∴平面 ⊥平面
⊥平面 . ------------------14分
. ------------------14分
20.解:(Ⅰ)易知,椭圆 的半焦距为:
的半焦距为: ,
,
又抛物线 的准线为:
的准线为: . ----------2分
. ----------2分
设双曲线M的方程为 ,依题意有
,依题意有 ,
,
故 ,又
,又 .
.
∴双曲线M的方程为 . ----------4分
. ----------4分
(Ⅱ)设直线 与双曲线M的交点为
与双曲线M的交点为 、
、 两点
两点
联立方程组 消去y得
消去y得  ,-------5分
,-------5分
∵ 、
、 两点的横坐标是上述方程的两个不同实根, ∴
两点的横坐标是上述方程的两个不同实根, ∴
∴
 ,
,
从而有 ,
, . ----------7分
. ----------7分
又 ,
,
∴ .
.
①
若


 ,则有
,则有
 ,即
,即
 .
.
∴当 时,使得
时,使得


 . ----------10分
. ----------10分
② 若存在实数 ,使A、B两点关于直线
,使A、B两点关于直线 对称,则必有
对称,则必有  ,
,
因此,当m=0时,不存在满足条件的k;
当 时,由
时,由 得
得 



∵A、B中点 在直线
在直线 上,
上,
∴ ,代入上式得
,代入上式得
 ,又
,又 , ∴
, ∴ ----------13分
----------13分
将 代入并注意到
代入并注意到 ,得
,得
 .
.
∴当 时,存在实数
时,存在实数 ,使A、B两点关于直线
,使A、B两点关于直线 对称----------14分
对称----------14分
21.解(I)三角形数表中前行共有个数,
第行最后一个数应当是所给奇数列中的第项。
故第行最后一个数是
因此,使得的m是不等式的最小正整数解。----------4分
由得
----------6分
于是,第45行第一个数是
----------7分
(II),。
故 ----------9分
第n行最后一个数是,且有n个数,若将看成第n行第一个数,则第n行各数成公差为-2的等差数列,故。
故
,
两式相减得:
----------13分
----------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com