（本小题满分12分）

甲、乙、丙、丁4名同学被随机地分到、、三个社区参加社会实践，要求每个社区至少有一名同学。

（Ⅰ）求甲、乙两人都被分到社区的概率；

（Ⅱ）求甲、乙两人不在同一个社区的概率；

（Ⅲ）设随机变量为四名同学中到社区的人数，求的分布列和的值。

（本小题满分12分）

甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试

合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设每人面试合格的概率都是，且面试是否合格互不影响.求：

（Ⅰ）至少有1人面试合格的概率;

（Ⅱ）签约人数的分布列和数学期望.

（本小题满分12分）

       甲、乙、丙三台机床各自独立的加工同一种零件，已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8，乙、丙两台机床加工的零件数相等，甲机床加工的零件数是乙机床加工的零件的二倍。

   （1）从甲、乙、丙加工的零件中各取一件检验，示至少有一件一等品的概率；

   （2）将三台机床加工的零件混合到一起，从中任意的抽取一件检验，求它是一等品的概率；

   （3）将三台机床加工的零件混合到一起，从中任意的抽取4件检验，其中一等品的个数记为X，求EX。

（本小题满分12分）

甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中甲胜乙的概率为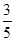，甲胜丙的概，乙胜丙的概率为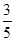，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束

网]

（本小题满分12分）

甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设甲面试合格的概率为，乙、丙面试合格的概率都是，且面试是否合格互不影响．求：

（Ⅰ）至少有1人面试合格的概率；

（Ⅱ）签约人数的分布列和数学期望．