
题目列表(包括答案和解析)
某项选拔共有两轮考核.第一轮笔试,设有五道选择题,每题答对得20分,答错或不答得0分,总分达到60分者进入第二轮考核,否则即被淘汰;第二轮面试,面试成绩服从正态分布![]() ,两轮总分达到150分及以上者即被录用.已知某选手能正确回答第一轮的每一道题的概率都是
,两轮总分达到150分及以上者即被录用.已知某选手能正确回答第一轮的每一道题的概率都是![]() ,且两轮中的各题能否正确回答互不影响,求该选手:
,且两轮中的各题能否正确回答互不影响,求该选手:
(I)笔试成绩ξ的分布列与数学期望;
(II)被录用的概率(参考数据:在标准正态分布中![]() )
)
湖南大学自主招生选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为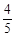 、
、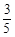 、
、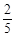 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望
(08年龙岩一中模拟理)(12分)
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为![]() 、
、![]() 、
、![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
在中央电视台所举办的北京2008年奥运火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为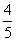 ,
,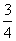 ,
,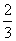 ,
, ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)该选手在选拔过程中回答过的问题的总个数记为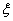 ,求随机变量
,求随机变量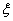 的分布列与数学期望.
的分布列与数学期望.
(1)求该选手进入第四轮才被淘汰的概率;
(2)该选手在选拔过程中回答过的问题的总个数记为ξ,求随机变量ξ的分布列与数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com