练习册

  • 练习册
  • 试题
    某汽车运输公司.购买了一批豪华大客车投入营运.据市场分析每辆客车营运的总利润与营运时间(年)的函数关系为.则每辆客车营运多少年.其运营的年利润最大A.2 B.3 C.4 D.5 【查看更多】

     

    题目列表(包括答案和解析)

    某汽车运输公司，购买了一批豪华大客车投入运营，据市场分析每辆客车运营前n（n∈N*）年的总利润Sn（单位：万元）与n之间的关系为Sn=-（n-6）2+11．当每辆客车运营的平均利润最大时，n的值为
    5
    5
    ．

    查看答案和解析>>

    某汽车运输公司，购买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y（单位：10万元）与营运年数x的函数关系为则每辆客车营运多少年，其运营的年平均利润最大为         .

    查看答案和解析>>

    某汽车运输公司，购买了一批豪华大客车投入客运，据市场分析，每辆客车营运利润y(10万元)与营运年数x(x∈N)为二次函数关系(图象如下图所示)，则每辆客车营运________年，其营运年平均利润最大.(    )

    A.3                   B.4                  C.5                 D.6

    查看答案和解析>>

    某汽车运输公司，购买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y(单位：万元)与营运年数x(x∈N)为二次函数关系(如图)，则每辆客车营运___________年，其营运的年平均利润最大.

      

    A.3                                 B.4                                     C.5                                 D.6

    查看答案和解析>>

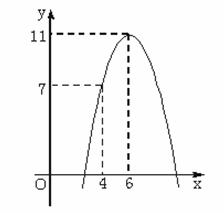
    某汽车运输公司，购买了一批豪华大巴投入客运，据市场分析，每辆客车营运的总利润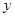（万元）与营运年数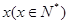满足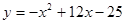，则每辆客车营运多少年使其营运年平均利润最大（      ）

    A、3年         B、4年        C、5年        D、6年

     

    查看答案和解析>>

    一、选择题

    C B B A B   A A A DD    C C

    二、填空题

    13.                               14.  ―4                     15. 2880                     16.①③

    17.解，由题意知，在甲盒中放一球概率为，在乙盒放一球的概率为   ….3分

    ①当n=3时，的概率为    …6分

    ②时，有或

    它的概率为     ….12分

    18.解： （1）解：在中  

                                                     2分

        4分

     

          

                                                           6分

     

    （2）=

         12分

     

    19. （法一）（1）证明：取中点，连接、．

           ∵△是等边三角形，∴⊥，

           又平面⊥平面，

           ∴⊥平面，∴在平面内射影是，

           ∵=2，，，,

           ∴△∽△，∴．

           又°，∴°，

           ∴°，∴⊥，

           由三垂线定理知⊥        ……….（6分）

    （2）取AP的中点E及PD的中点F，连ME、CF则CFEM为平行四边形，CF平面PAD所以ME平面PAD，所以平面MPA平面PAD所以二面角M―PA―D为900.（12分）

    20.解：（1）

                      2分

     

    -1

    (x)

    -

    0

    +

    0

    -

    (x)

    减

    极小值0

    增

    极大值

    减

                                   6分

     

    （2）

                                             8分

     

                                                                  12分

     

    21.Ⅰ）由题知点的坐标分别为，，

    于是直线的斜率为，

    所以直线的方程为，即为．…………………4分

     

    （Ⅱ）设两点的坐标分别为，

    由得，

    所以，．

    于是．

    点到直线的距离，

    所以.

    因为且，于是，

    所以的面积范围是．         …………………………………8分

    （Ⅲ）由（Ⅱ）及，，得

    ，，

    于是，（）.

    所以．

    所以为定值．               ……………………………………………12分

    22.解（Ⅰ）由得，

    数列{an}的通项公式为      4分

    （Ⅱ）

    设      ①

     

          ②

    ①―②得

    =

     

    即数列的前n项和为           9分

    （Ⅲ）解法1：不等式恒成立，

    即对于一切的恒成立

    设，当k>4时，由于对称轴，且而函数在是增函数，不等式恒成立

    即当k<4时，不等式对于一切的恒成立       14分

    解法2：bn=n(2n-1)，不等式恒成立，即对于一切恒成立

    而k>4

    恒成立，故当k>4时，不等式对于一切的恒成立 （14分）

     


    同步练习册答案