
题目列表(包括答案和解析)
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质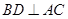 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面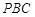 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m (m为正常数) 且
=m (m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求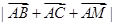 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求
为所求
第二问因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则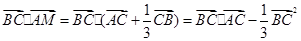 =
=
(2)当 时,则
时,则 =
=
第三问中,解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求……………2分
为所求……………2分
(Ⅱ)解:因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则 =
= ;-2分
;-2分
(2)当 时,则
时,则 =
= ;--2分
;--2分
(Ⅲ)解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令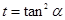 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
在数学证明中,①假言推理、②三段论推理、③传递关系推理、④完全归纳推理,是经常使用的四种演绎推理,下面推理过程使用到上述推理规则中的( )如(右图)

因为l AB,所以
AB,所以 又因为AB//CD,所以
又因为AB//CD,所以
所以
A. ①②③ B.②③④
C. ②③ D.①②③④
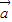 =(a1,a2),
=(a1,a2),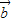 =(b1,b2),且
=(b1,b2),且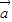 与
与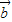 的夹角为θ,
的夹角为θ,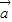 •
•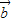 =|
=|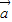 ||
||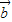 |cosθ,
|cosθ,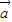 •
•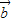 ≤|
≤|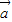 ||
||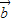 |.
|.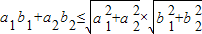 ,
,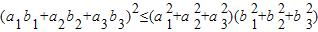 成立;
成立;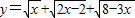 的最大值.
的最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com