
题目列表(包括答案和解析)
(本小题满分14分)如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() ,点E在棱PB
,点E在棱PB![]() 上
上![]() .(Ⅰ)求证:平面
.(Ⅰ)求证:平面![]() ;
; ![]() (Ⅱ)当
(Ⅱ)当![]() 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.
(本小题满分14分)
如图,四棱锥 中,
中,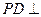 平面
平面 ,底面
,底面 为矩形,
为矩形, ,
,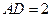 ,
, 为
为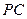 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥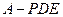 的体积;
的体积;
(Ⅲ) 边上是否存在一点
边上是否存在一点 ,使得
,使得 平面
平面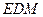 ,若存在,求出
,若存在,求出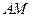 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.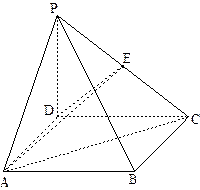
(本小题满分14分)
如图,四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,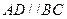 ,
, 侧面
侧面 ,△
,△ 是等边三角形,
是等边三角形,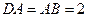 ,
, 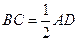 ,
, 是线段
是线段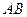 的中点.
的中点.
(Ⅰ)求证: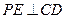 ;
;
(Ⅱ)求四棱锥 的体积;
的体积;
(Ⅲ)求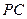 与平面
与平面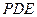 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)
如图,四棱锥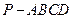 的底面
的底面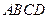 为菱形,
为菱形, 平面
平面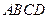 ,
,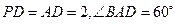 ,
,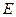 、
、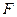 分别为
分别为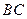 、
、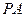 的中点。
的中点。
(I)求证: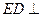 平面
平面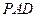 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥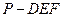 的体积;
的体积;
(Ⅲ)求平面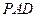 与平面
与平面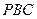 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.
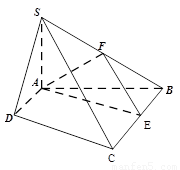
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足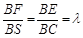 .(
.(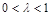 )
)
①求证:对于任意的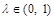 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在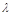 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的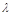 值;若不存在,说明理由.
值;若不存在,说明理由.
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
B
B
C
C
A
D
C
D
二、填空题(每小题5分,共20分)
11. 8 ; 12. AC⊥BD ( ABCD是正方形或菱形);
13. 数学文科.files/image211.gif) ; 14.
; 14. 数学文科.files/image213.gif) ;
;
三、解答题(本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)
解:(1) 数学文科.files/image215.gif) …………………………1分
…………………………1分
数学文科.files/image217.gif) ………………………………2分
………………………………2分
数学文科.files/image219.gif) . ………………………………………4分
. ………………………………………4分
数学文科.files/image221.gif) 的最小正周期是
的最小正周期是数学文科.files/image223.gif) . …………………………………6分
. …………………………………6分
(2)由数学文科.files/image142.gif) 得
得数学文科.files/image225.gif) …………………….8分
…………………….8分
∵数学文科.files/image227.gif) ,∴
,∴数学文科.files/image229.gif) ∴
∴数学文科.files/image231.gif) …………10分
…………10分
∴ 数学文科.files/image233.gif) ………………………………………………12分
………………………………………………12分
16.(本小题满分12分)
解:(1)当数学文科.files/image235.gif) 时,
时,数学文科.files/image237.gif) ,对任意
,对任意数学文科.files/image239.gif)
数学文科.files/image241.gif)
数学文科.files/image243.gif) 为偶函数 ……………………3分
为偶函数 ……………………3分
当数学文科.files/image245.gif) 时,
时,数学文科.files/image247.gif)
取数学文科.files/image249.gif) ,得
,得 数学文科.files/image251.gif)
数学文科.files/image253.gif)
数学文科.files/image255.gif) 函数
函数数学文科.files/image110.gif) 既不是奇函数,也不是偶函数……6分
既不是奇函数,也不是偶函数……6分
(2)解法一:要使函数数学文科.files/image110.gif) 在
在数学文科.files/image152.gif) 上为增函数等价于
上为增函数等价于数学文科.files/image258.gif) 在
在数学文科.files/image152.gif) 上恒成立 ……………8分
上恒成立 ……………8分
即数学文科.files/image260.gif) 在
在数学文科.files/image152.gif) 上恒成立,故
上恒成立,故数学文科.files/image262.gif) 在
在数学文科.files/image152.gif) 上恒成立
上恒成立
∴数学文科.files/image264.gif) …………………………………10分
…………………………………10分
∴ 数学文科.files/image154.gif) 的取值范围是
的取值范围是数学文科.files/image267.gif) ………………………………12分
………………………………12分
解法二:设数学文科.files/image269.gif)
数学文科.files/image271.gif)
数学文科.files/image273.gif) ………8分
………8分
要使函数数学文科.files/image110.gif) 在
在数学文科.files/image152.gif) 上为增函数,必须
上为增函数,必须数学文科.files/image276.gif) 恒成立
恒成立
数学文科.files/image278.gif) ,即
,即数学文科.files/image280.gif) 恒成立 …………………………………10分
恒成立 …………………………………10分
又数学文科.files/image282.gif) ,
,数学文科.files/image284.gif)
数学文科.files/image286.gif)
数学文科.files/image288.gif)
数学文科.files/image290.gif) 的取值范围是
的取值范围是数学文科.files/image267.gif) ………………………………12分
………………………………12分
17.(本小题满分14分)
证明: (1)取PC的中点G,连结FG、EG
∴FG为△CDP的中位线 ∴FG数学文科.files/image292.gif) CD……1分
CD……1分
∵四边形ABCD为矩形,E为AB的中点
∴AB数学文科.files/image292.gif) CD ∴FG
CD ∴FG数学文科.files/image295.gif) AE
AE
∴四边形AEGF是平行四边形 ………………2分
∴AF∥EG ………3分
又EG数学文科.files/image297.gif) 平面PCE,AF
平面PCE,AF数学文科.files/image299.gif) 平面PCE ………4分
平面PCE ………4分
∴AF∥平面PCE ………………………………………5分
(2)∵ PA⊥底面ABCD
∴PA⊥AD,PA⊥CD,又AD⊥CD,PA数学文科.files/image301.gif) AD=A
AD=A
∴CD⊥平面ADP
又AF数学文科.files/image297.gif) 平面ADP
∴CD⊥AF ……………………………… 6分
平面ADP
∴CD⊥AF ……………………………… 6分
直角三角形PAD中,∠PDA=45°
∴△PAD为等腰直角三角形 ∴PA=AD=2 ………………………… 7分
∵F是PD的中点
∴AF⊥PD,又CD数学文科.files/image301.gif) PD=D
PD=D
∴AF⊥平面PCD ……………………………… 8分
∵AF∥EG
∴EG⊥平面PCD …………………………… 9分
又EG数学文科.files/image297.gif) 平面PCE
平面PCE
平面PCE⊥平面PCD …………………………… 10分
(3)三棱锥C-BEP即为三棱锥P-BCE ……………………………11分
PA是三棱锥P-BCE的高,
Rt△BCE中,BE=1,BC=2,
∴三棱锥C-BEP的体积
VC-BEP=VP-BCE=数学文科.files/image306.gif) … 14分
… 14分
18.(本小题满分14分)
解:(1)由已知得数学文科.files/image308.gif) 解得
解得数学文科.files/image310.gif) .…………………1分
.…………………1分
设数列数学文科.files/image158.gif) 的公比为
的公比为数学文科.files/image313.gif) ,由
,由数学文科.files/image310.gif) ,可得
,可得数学文科.files/image316.gif) .
.
又数学文科.files/image164.gif) ,可知
,可知数学文科.files/image319.gif) ,即
,即数学文科.files/image321.gif) , …………………4分
, …………………4分
解得数学文科.files/image323.gif) .
.
由题意得数学文科.files/image325.gif) .
. 数学文科.files/image327.gif) .…………………………………………
6分
.…………………………………………
6分
故数列数学文科.files/image158.gif) 的通项为
的通项为数学文科.files/image330.gif) . …
……………………………………8分
. …
……………………………………8分
(2)由于数学文科.files/image173.gif) 由(1)得
由(1)得数学文科.files/image333.gif)
数学文科.files/image335.gif) =
=数学文科.files/image337.gif) ………………………………………10分
………………………………………10分
又数学文科.files/image339.gif)
数学文科.files/image341.gif) 是首项为
是首项为数学文科.files/image343.gif) 公差为
公差为数学文科.files/image343.gif) 的等差数列
……………12分
的等差数列
……………12分
数学文科.files/image345.gif)
数学文科.files/image347.gif) …………………………14分
…………………………14分
19.(本小题满分14分)
数学文科.files/image349.gif) 解:(1)如图,设
解:(1)如图,设数学文科.files/image351.gif) 为动圆圆心,
为动圆圆心, 数学文科.files/image353.gif)
数学文科.files/image355.gif) ,过点
,过点数学文科.files/image351.gif) 作直线
作直线数学文科.files/image357.gif) 的垂线,垂足为
的垂线,垂足为数学文科.files/image359.gif) ,由题意知:
,由题意知: 数学文科.files/image361.gif) ……………………………………2分
……………………………………2分
即动点数学文科.files/image351.gif) 到定点
到定点数学文科.files/image353.gif) 与到定直线
与到定直线数学文科.files/image357.gif) 的距离相等,
的距离相等,
由抛物线的定义知,点数学文科.files/image351.gif) 的轨迹为抛物线,其中
的轨迹为抛物线,其中数学文科.files/image365.gif) 为焦点,
为焦点,
数学文科.files/image357.gif) 为准线,
为准线,
∴动圆圆心的轨迹方程为数学文科.files/image368.gif) ……………………………………5分
……………………………………5分
(2)由题可设直线数学文科.files/image186.gif) 的方程为
的方程为数学文科.files/image371.gif)
由数学文科.files/image373.gif) 得
得数学文科.files/image375.gif)
△数学文科.files/image377.gif) ,
,数学文科.files/image379.gif) ………………………………………………7分
………………………………………………7分
设数学文科.files/image381.gif) ,
,数学文科.files/image383.gif) ,则
,则数学文科.files/image385.gif) ,
,数学文科.files/image387.gif) ………………………9分
………………………9分
由数学文科.files/image191.gif) ,即
,即 数学文科.files/image390.gif) ,
,数学文科.files/image392.gif) ,于是
,于是数学文科.files/image394.gif) ,……11分
,……11分
即数学文科.files/image396.gif) ,
,数学文科.files/image398.gif) ,
,
数学文科.files/image400.gif) ,解得
,解得数学文科.files/image402.gif) 或
或数学文科.files/image404.gif) (舍去), …………………13分
(舍去), …………………13分
又数学文科.files/image406.gif) , ∴ 直线
, ∴ 直线数学文科.files/image186.gif) 存在,其方程为
存在,其方程为数学文科.files/image409.gif) ……………14分
……………14分
20.(本小题满分14分)
解:(1)由已知,得数学文科.files/image411.gif) ,比较两边系数,
,比较两边系数,
得数学文科.files/image413.gif) . ……………………4分
. ……………………4分
(2)令数学文科.files/image415.gif) ,要
,要数学文科.files/image417.gif) 有三个不等的实数根,则函数
有三个不等的实数根,则函数数学文科.files/image110.gif) 有
有
一个极大值和一个极小值,且极大值大于0,极小值小于0. …………5分
由已知,得数学文科.files/image419.gif) 有两个不等的实根
有两个不等的实根数学文科.files/image052.gif) ,
,
数学文科.files/image422.gif) ,
,数学文科.files/image424.gif) 得
得数学文科.files/image426.gif) .……… 6分
.……… 6分
又数学文科.files/image428.gif) ,
,数学文科.files/image430.gif) ,将
,将数学文科.files/image432.gif) 代入(1)(3),有
代入(1)(3),有数学文科.files/image434.gif) ,又
,又数学文科.files/image436.gif)
数学文科.files/image438.gif) .
.数学文科.files/image440.gif) ,
………8分
,
………8分
则数学文科.files/image442.gif) ,且
,且数学文科.files/image110.gif) 在
在数学文科.files/image445.gif) 处取得极大值,在
处取得极大值,在数学文科.files/image447.gif) 处取得极小值10分 故
处取得极小值10分 故数学文科.files/image417.gif) 要有三个不等的实数根,
要有三个不等的实数根,
则必须数学文科.files/image450.gif) ………………
12分
………………
12分
解得数学文科.files/image452.gif) .
………………… 14分
.
………………… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com