
题目列表(包括答案和解析)
对于具有相同定义域![]() 的函数
的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (
(![]() 为常数),对任给的正数
为常数),对任给的正数![]() ,存在相应的
,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() 则称直线
则称直线![]()
![]() 为曲线
为曲线![]() 与
与![]() 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D=![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;②
;②![]() ,
,![]()
![]() ;
;
③![]()
![]() ,
,![]()
![]() ;④
;④![]() ,
,![]() 。
。
其中,曲线![]() 与
与![]() 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
对于具有相同定义域![]() 的函数
的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (
(![]() 为常数),对任给的正数
为常数),对任给的正数![]() ,存在相应的
,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() 则称直线
则称直线![]()
![]() 为曲线
为曲线![]() 与
与![]() 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D=![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;②
;②![]() ,
,![]()
![]() ;
;
③![]()
![]() ,
,![]()
![]() ;④
;④![]() ,
,![]() 。
。
其中,曲线![]() 与
与![]() 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
对于具有相同定义域D的函数f(x)和g(x),若存在函数h(x)=kx+b(k,b为常数),对任给的正数m,存在相应的x0 D,使得当x
D,使得当x D且x>x0时,总有
D且x>x0时,总有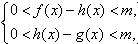 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=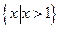 的四组函数如下:
的四组函数如下:
①f(x)=x2,g(x)=  ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 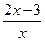 ;
;
③f(x)= 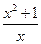 ,g(x)=
,g(x)= 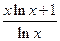 ; ④f(x)=
; ④f(x)= 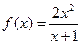 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).
其中,曲线y=f(x)与y=g(x)存在“分渐近线”的是
| A.①④ | B.②③ | C.②④ | D.③④ |
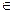 D,使得当x
D,使得当x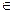 D且x>x0时,总有
D且x>x0时,总有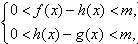 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=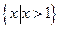 的四组函数如下:
的四组函数如下: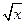 ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 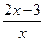 ;
;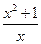 ,g(x)=
,g(x)= 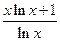 ; ④f(x)=
; ④f(x)= 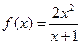 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).| A.①④ | B.②③ | C.②④ | D.③④ |
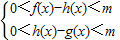 ,则称直线l:y=ka+b为曲线y=f(x)和y=g(x)的“分渐进性”.给出定义域均为D={x|x>1}的四组函数如下:
,则称直线l:y=ka+b为曲线y=f(x)和y=g(x)的“分渐进性”.给出定义域均为D={x|x>1}的四组函数如下: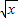 ②f(x)=10-x+2,g(x)=
②f(x)=10-x+2,g(x)=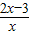 ③f(x)=
③f(x)=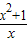 ,g(x)=
,g(x)=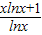 ④f(x)=
④f(x)=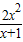 ,g(x)=2(x-1-e-x)
,g(x)=2(x-1-e-x)1.  2. 1 3. 4 4.
2. 1 3. 4 4.  5. 1, 6. 90° 7. 13
5. 1, 6. 90° 7. 13
8.  9.
9.  10. 4
11. y=2x 12. 9
10. 4
11. y=2x 12. 9
13. D 14. B 15. D 16. C
17. 解: (1)y=2sin(2x- ),
), 
(2)

 ……
……
∴函数y的值域为[-1,2]
……………
18. (1)解 如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
在△A′CP中,
 易得A′C=
易得A′C= a,CP=DE=
a,CP=DE= a,A′P=
a,A′P= a
a
由余弦定理得cosA′CP=




(2)解 ∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上 如下图所示
如下图所示
 又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′
在Rt△B′AD中,AD= a,AB′=
a,AB′= a,B′D=
a,B′D= a
a
则cosADB′=
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上 如下图所示
如下图所示
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′,
如图建立坐标系,则



 ,
,
19. (1)解 为等差数列,
为等差数列,
 ……………………………………………………2分
……………………………………………………2分
解得 ……………………………4分
……………………………4分
 ………………………………………………………………5分
………………………………………………………………5分
 ……………………………………………………………6分
……………………………………………………………6分
(2) ………………………………………………6分
………………………………………………6分

 …………8分
…………8分
因 ,知
,知 上单减,在
上单减,在 上单增,
上单增,
又 ,
,
而 …………………………………………10分
…………………………………………10分
∴当n =
5时, 取最大值为
取最大值为 ………………12分
………………12分
20. 解:(1)∵ ,∴
,∴ ,即
,即 ,
,
∵ ,∴
,∴
(2) ,
, 
当 ,
,
即 时,
时,
当 时,∵
时,∵ ,∴这样的
,∴这样的 不存在。
不存在。
当 ,即
,即 时,
时, ,这样的
,这样的 不存在。
不存在。
综上得,
 .
.
21. 解:(1) Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
 GQ为PN的中垂线
GQ为PN的中垂线 |PG|=|GN|
|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长 ,半焦距
,半焦距 ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是
(2)因为 ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得| |=|
|=| |,则四边形OASB为矩形
|,则四边形OASB为矩形
若l的斜率不存在,直线l的方程为x=2,由
 矛盾,故l的斜率存在.
矛盾,故l的斜率存在.
设l的方程为

 ①
①

 ②
②
把①、②代入
∴存在直线 使得四边形OASB的对角线相等.
使得四边形OASB的对角线相等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com