tesoon 三、解答题; 17.(10分) ∵.files/image133.gif) ∴ ∴.files/image135.gif) …..3分 …..3分 由.files/image137.gif) 得, 得,.files/image139.gif) 即 即.files/image141.gif) 当.files/image143.gif) 时, 时,.files/image145.gif) ; 6分 当 ; 6分 当.files/image147.gif) 时, 时,.files/image149.gif) ……..10分 ……..10分 18.(12分) (1)取PD的中点E,连接AE、EN .files/image151.jpg) ∵EN平行且等于 ∵EN平行且等于.files/image153.gif) DC,而 DC,而.files/image153.gif) DC平行且等于AM DC平行且等于AM
∴AMNE为平行四边形MN∥AE ∴MN∥平面PAD (6分) (2)∵PA⊥平面ABCD∴CD⊥PA又 ∵ABCD为矩形,∴CD⊥AD ∴CD⊥AE,AE∥MN,MN⊥CD (3分) ∵AD⊥DC,PD⊥DC ∴∠ADP=45° 又E是斜边的PD的中点∴AE⊥PD, ∴MN⊥PD∴MN⊥CD,∴MH⊥平面PCD.(6分) 19.(12分) (1).files/image155.gif) 所以.files/image157.gif) …….. 6分
…….. 6分 (2).files/image159.gif) 因为.files/image161.gif) 所以,.files/image163.gif) 即 即.files/image165.gif) 20.(12分) (1)由题意知.files/image167.gif) 当.files/image169.gif) .files/image171.gif) ……………………2分 ……………………2分 当.files/image173.gif) 两式相减得.files/image175.gif) 整理得: 整理得:.files/image177.gif) ……..4分
……..4分 .files/image179.gif) 是以2为首项,2为公比的等比数列, 是以2为首项,2为公比的等比数列,.files/image181.gif) ……. 6分 ……. 6分
(2)由(1)知.files/image183.gif) .files/image185.gif) ……..1分 ……..1分 .files/image187.gif) ① ①
.files/image189.gif) ② ②
①―②得.files/image191.gif) ……… 9分 ……… 9分 .files/image193.gif) …4分 …4分.files/image195.gif) ………6分
………6分
21.(12分) (1)由题有.files/image197.gif) ,∵ ,∵.files/image199.gif) 是 是.files/image201.gif) 的两个极值点, 的两个极值点, ∴.files/image199.gif) 是方程 是方程.files/image203.gif) 的两个实根, 的两个实根, ∵a>0,∴.files/image205.gif) ∴.files/image207.gif) 又∵.files/image209.gif) ,∴ ,∴.files/image211.gif) ,即 ,即.files/image213.gif) ; ..6分 ; ..6分 (2)令.files/image215.gif) ,则 ,则.files/image217.gif) 由.files/image219.gif) ,由 ,由.files/image221.gif) , , 故.files/image223.gif) 在 在.files/image225.gif) 上是增函数,在区间 上是增函数,在区间.files/image227.gif) 上是减函数, ∴ 上是减函数, ∴.files/image229.gif) , , 即.files/image231.gif) ,∴b的最大值是 ,∴b的最大值是.files/image233.gif) . …..6分 . …..6分 22.(12分) (1)抛物线.files/image235.gif) 的准线 的准线.files/image237.gif) ,于是,4+ ,于是,4+.files/image239.gif) =5,∴p=2. =5,∴p=2. ∴抛物线方程为.files/image241.gif) . (4分) . (4分) (2)∵点A的坐标是(4,4),由题意得B(0,4),M(0,2).又∵F(1,0), ∴.files/image243.gif) ,又MN⊥FA,∴ ,又MN⊥FA,∴.files/image245.gif) ,则FA的方程为 ,则FA的方程为.files/image247.gif) MN的方程为.files/image249.gif) ,解方程组 ,解方程组.files/image251.gif) 得, 得,.files/image253.gif) ∴N.files/image255.gif) …..4分 …..4分 (3)由题意得,圆M的圆心是点(0,2),半径为2. 当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离. 当.files/image257.gif) 时,直线AK的方程为 时,直线AK的方程为.files/image259.gif) 即为 即为.files/image261.gif) , , 圆心M(0,2)到直线AK的距离.files/image263.gif) ,令d>2.解得m>1, ,令d>2.解得m>1, 所以,当m>1时,直线AK与圆M相离;当m=1时,直线AK与圆M相切, 当m<1时,直线AK与圆M相交.
………. 4分
| |

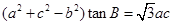 ,则角B的值为____________
,则角B的值为____________ ,则角B的值为____________
,则角B的值为____________