题目列表(包括答案和解析)
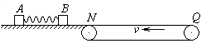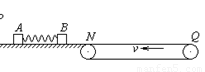
如图所示，光滑水平面MN上放两相同小物块A、B，右端N处与水平传送带理想连接，传送带水平部分长度L=8m，沿逆时针方向以恒定速度v=2m/s匀速转动．物块A、B（大小不计）与传送带间的动摩擦因数μ=0.2．物块A、B质量mA=mB=1kg．开始时A、B静止，A、B间压缩一轻质弹簧，蓄有弹性势能Ep=16J．现解除锁定，弹开A、B，弹开后弹簧掉落，对A、B此后的运动没有影响．g=10m/s2，求：如图所示，光滑水平面MN上放两相同小物块A、B，右端N处与水平传送带理想连接，传送带水平部分长度L=8m，沿逆时针方向以恒定速度v =2m/s匀速转动。物块A、B（大小不计）与传送带间的动摩擦因数
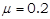。物块A、B质量mA=mB=1kg。开始时A、B静止，A、B间压缩一轻质弹簧，蓄有弹性势能Ep=16J。现解除锁定，弹开A、B，弹开后弹簧掉落，对A、B此后的运动没有影响。g=10m/s2，求：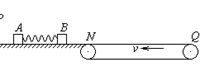
（1）物块B沿传送带向右滑动的最远距离；
（2）物块B从滑上传送带到回到水平面所用的时间。
如图所示，光滑水平面MN上放两相同小物块A、B，右端N处与水平传送带理想连接，传送带水平部分长度L=8m，沿逆时针方向以恒定速度v =2m/s匀速转动。物块A、B（大小不计）与传送带间的动摩擦因数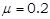
。物块A、B质量mA=mB=1kg。开始时A、B静止，A、B间压缩一轻质弹簧，蓄有弹性势能Ep=16J。现解除锁定，弹开A、B，弹开后弹簧掉落，对A、B此后的运动没有影响。g=10m/s2，求：
（1）物块B沿传送带向右滑动的最远距离；
（2）物块B从滑上传送带到回到水平面所用的时间。
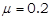。物块A、B质量mA=mB=1kg。开始时A、B静止，A、B间压缩一轻质弹簧，蓄有弹性势能Ep=16J。现解除锁定，弹开A、B，弹开后弹簧掉落，对A、B此后的运动没有影响。g=10m/s2，求：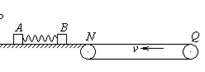
某同学用图1的实验装置探究“小车加速度与力”的关系，图中A为小车，连接在后面的纸带穿过打点计时器B的限位孔，它们均置于水平放置的一端带有定滑轮的足够长的木板上，C为弹簧测力计，P为带有滑轮及砝码的盘，通过增减盘中的砝码可调节A受到的拉力。实验中，小车碰到定滑轮时，盘和砝码尚未到达地面。
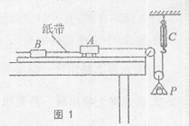
（1）调节P中的砝码，先接通电源、再松开小车，观察发现弹簧测力计C的示数如图2时，打 点计时器打下的纸带如图3所示，已知打点计时器工作频率为50Hz，可求得：（保留三位有效数字）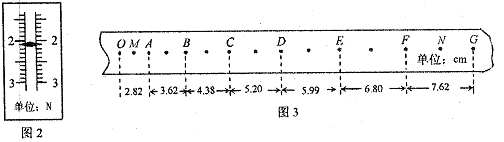
①滑块运动的加速度a= ；
②小车A的质量为mA= ，与真实值相比，求得小车A的质量 （选填“偏大”或“偏小”）．写出支持你的看法的一个论据： 。
（2）利用此装置还可以验证A、P组成的系统机械能是否守恒，若选用图3中纸带上的M、N两点进行验证，已知小车A的质量为mA，回答下列问题：（重力加速度为g）
①下列物理量中，还需测量或计算的是 ．（填入正确选项前的字母）
A．P的总质量mP B．M点的速度vM和N点的速度vN
G．OG两点间的距离hOG D．MN两点间的距离hMN
E．小车从M运动到N的时间t AN
②AP系统从M到N的过程中，重力势能的减小量为△Ep= ，动能的增加量为△Ek= ．（用测量或计算的物理量字母表示）
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷。
第Ⅰ卷共18小题，每题6分．共108分。
一、选择题：选对的给6分，选错的或未选得给0分。
1.C 2.D 3.A 4.A 5.B 6.D 7.C 8.B 9.C 10.D 11.B 12.C
二、选择题：全部选对的给6分，选对但不全的给3分，有选错得或未选的给0分。
13.C 14.A、D 15.D 16.B 17.A、D 18.D
第Ⅱ卷必考部分共9题，共157分。
19.(18分)
（1）1.996～1.998 （2分） 1.094（2分）
（2）保护电源，防止短路（2分）
（3）如右图所示（有一处错就不给分）（4分）
（4）2.9；1.0（4分）
（5）多测几组R、U，分别求出电动势E、内阻r，再求E、r的平均值（2分）；
或利用U-I图象处理数据。（2分）
20.（15分）
解：（1）解除锁定弹开物块AB后，两物体的速度大小
①（2分）
弹簧储存的弹性势能
②（3分）
（2）物块B滑上传送带匀减速运动，当速度减为零时，滑动的距离最远．
由动能定理得：
③（2分）
得：
④（2分）
（3）物块B沿传送带向左返回时，先匀加速运动，物块速度与传送带速度相同时再一起匀速运动，设物块B加速到传送带速度v需要滑动的距离为
由
得
⑤（3分）
表明物块B滑回水平面MN的速度没有达到传送带的速度
所以: 
⑥（3分）
21.（19分）
解：（1）输电线冰层的体积V冰 = πR2L （2分）
由对称关系可知，塔尖所受压力的增加值等于一根导线上冰层的重力，即
Δm = ρV冰 g= πρR2Lg （2分）
（画出受力图示正确给4分）
（2）输电线与冰层的总质量M' = m0L + πρR2Lg，（1分）
输电线受力如图甲所示。
由共点力的平衡条件，得2F1cosθ = m0Lg + πρR2Lg （3分）
输电线在最高点所受的拉力
（2分）
半根输电线的受力如图乙所示。
由共点力的平衡条件，得F2 = F1sinθ （3分）
输电线在最低点所受的拉力
（2分）
22.（20分）
解：（1）电场力与洛伦兹力平衡得：qE=qv0B得：E=v0B 方向竖直向上 （2分）
（2）根据运动的对称性，微粒能从P点到达Q点，应满足
（2分）
其中x为每次偏转圆弧对应的弦长，偏转圆弧对应的圆心角为
或
． （2分）
设圆弧的半径为R，则有2R2=x2，可得：
（2分）
又
由①②③式得：
，n=1、2、3、……
（2分）
（3）当n取奇数时，微粒从P到Q过程中圆心角的总和为
，（2分）
，其中n=1、3、5、…（2分）
当n取偶数时，微粒从P到Q过程中圆心角的总和为：
，（2分）
，其中n=2、4、6、……（2分）
欲使时间最小，取n=1或者2，此时
（2分）
23.（15分）
解：（1）H （1分）
（2） （1分）
（3）3Cu + 2NO3- + 8H+ === 3Cu2+ + 2NO↑ + 4H2O（3分）
（4）①
NH4+ + OH- H2O +
NH3 ↑ （2分）
② SO32- + Cl2 + H2O = SO42- + 2Cl- + 2H+ （3分）
（5）① (NH4)2Fe(SO4)2?6H2O （2分）
② 5Fe2+ + MnO4- + 8H+ ＝ 5Fe3++ Mn2+ + 4H2O （3分）
24.（15分）
解：⑴2CNO－+2H++3ClO－=N2↑+2CO2↑+3Cl－+H2O（2分）
|
（2分）；
立毛肌（1分）
（2分）
酯化反应（或取代反应）