
题目列表(包括答案和解析)
已知各项都不为零的数列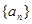 的前n项和为
的前n项和为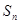 ,
,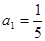 ,向量
,向量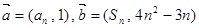 ,其中
,其中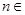 N*,且
N*,且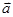 ∥
∥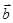 .
.
(Ⅰ)求数列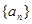 的通项公式及
的通项公式及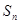 ;
;
(Ⅱ)若数列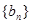 的前n项和为
的前n项和为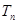 ,且
,且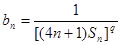 (其中
(其中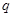 是首项
是首项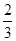 ,第四项为
,第四项为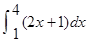 的等比数列的公比),求证:
的等比数列的公比),求证: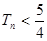 .
.
【解析】本试题主要考查了数列的通项公式和前n项和公式的运用。
(1)因为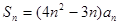 ,对n=1,
,对n=1, 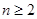 分别求解通项公式,然后合并。利用
分别求解通项公式,然后合并。利用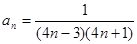 ,求解
,求解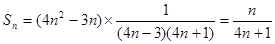
(2)利用
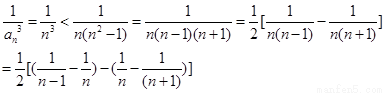
裂项后求和得到结论。
解:(1) 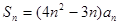 ……1分
……1分
当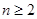 时,
时,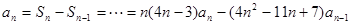 ……2分
……2分
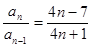 (
(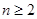 )……5分
)……5分
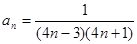 ……7分
……7分
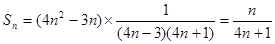 ……9分
……9分
证明:当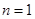 时,
时,
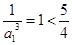
当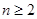 时,
时,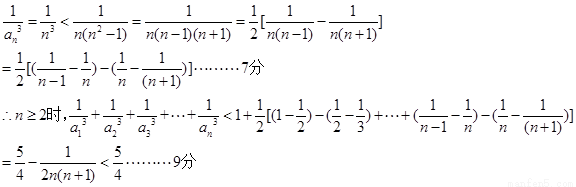
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列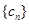 的前
的前 项和
项和 .
.
【解析】第一问利用由 得
得
两式相减得
故 时,
时,
从而 又
又 即
即 ,而
,而
从而 故
故
第二问中,
 又
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为
第三问中,
 两边同乘以
两边同乘以
利用错位相减法得到和。
(1)由 得
得
两式相减得
故 时,
时,
从而 ………………3分
………………3分
又 即
即 ,而
,而
从而 故
故
 对任意
对任意 ,
, 为常数,即
为常数,即 为等比数列………………5分
为等比数列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为 ………………9分
………………9分
(3)
 两边同乘以
两边同乘以
 ………………11分
………………11分
两式相减得

已知数列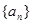 的前n项和
的前n项和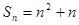 ,数列
,数列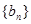 有
有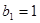 ,
,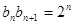
(1)求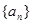 的通项;
的通项;
(2)若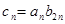 ,求数列
,求数列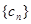 的前n项和
的前n项和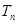 .
.
【解析】第一问中,利用当n=1时,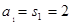
当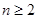 时,
时,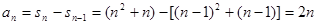
得到通项公式
第二问中,∵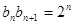 ∴
∴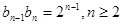 ∴数列
∴数列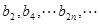 是以2为首项,2为公比的等比数列,利用错位相减法得到。
是以2为首项,2为公比的等比数列,利用错位相减法得到。
解:(1)当n=1时,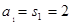 ……………………1分
……………………1分
当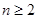 时,
时,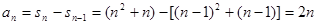 ……4分
……4分
又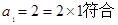
∴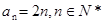 ……………………5分
……………………5分
(2)∵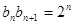 ∴
∴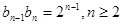
∴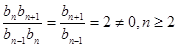 ……………………7分
……………………7分
又∵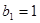 ,
,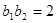 ∴
∴ 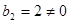
∴数列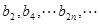 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,
∴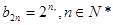 ……………………9分
……………………9分
∴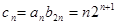
∴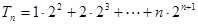 ①
①
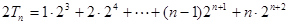 ②
②
①-②得: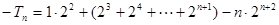
∴
某市投资甲、乙两个工厂,2011年两工厂的产量均为100万吨,在今后的若干年内,甲工厂的年产量每年比上一年增加10万吨,乙工厂第 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 年的年产量分别为
年的年产量分别为 万吨和
万吨和 万吨.
万吨.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若某工厂年产量超过另一工厂年产量的2倍,则将另一工厂兼并,问到哪一年底,其中哪一个工厂被另一个工厂兼并.
【解析】本试题主要考查数列的通项公式的运用。
第一问由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二问,考查等差数列与等比数列的综合,考查用数列解决实际问题,其步骤是建立数列模型,进行计算得出结果,再反馈到实际中去解决问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.
解:(Ⅰ)由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的产量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工厂将被乙工厂兼并
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com